平面での相対速度は「相手-自分」の公式が使えません。
平面での相対速度は
step1:同じところから移動していることにする
step2:「自分」から「相手」へ目線を引く
step3:目線の長さと向きが相対速度を表す
の手順に従って解いていきます。
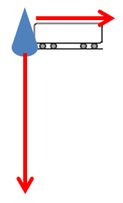
step1:
まず、問題に登場する観測者(電車)と雨粒が同じところにいたとします。
図では雨粒のサイズ感がおかしいですが、まあ、あれです。きっと遠近法です。
大きさの違いは特に気にしないでください。同じところから動き始めたとします。
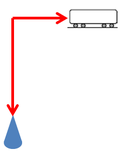
しばらくして動いていくと、こういう図になりますね。
雨粒が地下のどこかに行っているように見えますが、あくまで概念の話なので、進んだとしたらどうなるかという図です。

step2:
この問題では、電車内の観測者が雨粒を見ているわけですので、電車から雨粒を見ているとして、目線を矢印で引いてやります。そうすると確かに問題のイラストと同じように、鉛直方向に降っているはずの雨が斜め後ろ方向に落下しているように見えますね。
step3:
しかもこの角度が鉛直方向からきれいに30°ということですので、\(1:2:\sqrt{3}\)の直角三角形が作図されていることになります。辺の長さが速さを表しますので、電車の速さが\(5.0m/s\)ということであれば、\(1:\sqrt{3}\)の関係で、雨粒が落ちる速さはその\(\sqrt{3}\)倍となります。
よって、地面に対する雨粒の速さは
\(5.0×\sqrt{3}\)
\(≒5.0×1.73\)
\(=8.65\)
\(≒8.7m/s\)
となります。
問題文が有効数字2ケタなので、解答も2ケタ分だけ残して、あとは四捨五入してしまいましょう。
