ここまで、光は波なのか粒子なのかという議論がなされており、粒子である証拠が集まりつつあります。ここで新しい知見が発見されました。同じ電磁波の中で、X線もどうやら波ではなく粒子であるという証拠が発見されました。
これに関する理論的な説明がコンプトン効果です。
■非破壊検査
ある試料があったとして、この物質や成分が何であるかを調べる方法は様々なものがあります。しかし、薬品と反応させて溶かしたり、粉々にして粉末の性質を確かめたりして検査するには、試料を一度壊さないといけません。この破壊なしで試料の成分や構造を分析する検査法を非破壊検査と呼びます。
具体的には、電流を流してみたり、レントゲン写真を撮って内部を見たり、X線を照射して反射X線の様子をとらえたりするなどの方法があります。今回は、このうち反射X線について、不思議な性質があることを深掘りしてみようとおもいます。
■コンプトン効果
ある試料に波長λのX線を照射しました。すると、試料に当たって反射されるものと、そのまま透過して裏側に進むものとがありました。ところが、これとは別に角度θで斜め後ろに進むX線や、グイっと曲がって手前方向に斜めに返ってくるX線があることも観測されました。
これに関する明快な説明としては、結晶面とミラー指数という単元ありますが、ここではそれは飛ばします。入射光と反射光が一致せず、斜めに反射する何らかの理由は既に得られているわけです。
ところが、その斜めに反射するX線の波長を調べると、入射X線の波長よりわずかに長いことが実験で確かめられました。この「わずかな」変化とは具体的には\(10^{-12}m\)くらい長くなる変化です。
▼コンプトン効果
\(Δλ=\displaystyle\frac{h}{mc}(1-cosθ)[m]\)
\(Δλ=2.4×10^{-12}(1-cosθ)[m]\)
■量子学的エネルギー・運動量
Planckの量子仮説とEinsteinの光量子仮説により、1つのX線"粒子"が持つエネルギーは\(E=hν\)であることが知られています。
同様に、Einsteinの相対性理論により、その運動量は\(p=\frac{hν}{c}\)であることも知られました。量子仮説が1901年、光量子仮説が1905年、相対性理論が1916年ですので、コンプトン効果が研究されていた1923年頃にはすでに知られていた数式です。コンプトンらは、この新しい理論による数式をフル活用してコンプトン効果をまとめ上げたのです。
実際はコンプトン一人の業績ではなく、X線分析のデバイシェラー環で名前を残しているデバイという科学者がコンプトンの理論の穴を補って、ようやく完全なものとなっているのですが、このデバイは、ぜひともコンプトン氏の名前のみを残してあげてほしい、私が研究したことは大したことではない、として「コンプトンデバイ効果」とはならなかったわけです。
後年、コンプトンはこの業績に対してノーベル賞を受賞しますが、デバイへの受賞はありませんでした。ところがデバイはノーベル化学賞のほうを受賞しています。神様はすべてを見ているのかもしれませんね。
▼量子学的エネルギー・運動量
\(E=hν=\displaystyle\frac{hc}{λ}\)
\( p=\displaystyle\frac{hν}{c}=\frac{h}{λ}\)
■Compton効果の証明
この証明は発展項目です。中堅国公立~難関私立大あたりでは出題されているのを見かけますが、空欄補充になっていて、最初から最後までを導出させるような問題は見ませんので、キーになる部分だけ押さえていれば十分でしょう。中堅私立大から下の偏差値帯の大学では、そもそも出題すらされないところも多いので、入試要項と過去問をよく見て、出題の可能性が低そうだったら、ここにあてる勉強時間を他に回した方がいいかもしれません。
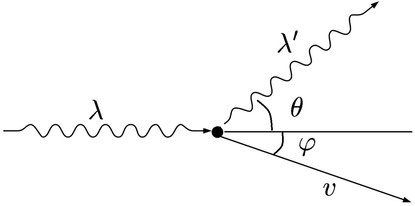
入射X線のエネルギーと運動量
\((E_0,p_0)=(\displaystyle\frac{hc}{λ} , \frac{h}{λ})\)
散乱X線のエネルギーと運動量
\((E_X,p_X)=(\displaystyle\frac{hc}{λ'} , \frac{h}{λ'})\)
散乱電子のエネルギーと運動量
\((E_e,p_e)=(\displaystyle\frac{1}{2}mv^2 , mv)\)
と書けるので、エネルギーと運動量について、それぞれ保存則を立てることにします。
①エネルギー保存則
\(\displaystyle\frac{hc}{λ}=\frac{hc}{λ'}+\frac{1}{2}mv^2\)
②x軸方向の運動量保存則
\(\displaystyle\frac{h}{λ}=\frac{h}{λ'}cosθ+mvcosφ\)
③y軸方向の運動量保存則
\(0=\frac{h}{λ'}sinθ-mvsinφ\)
ここからの解答指針として、
②③からφを消去
↓
①を変形してmvの形を作る
↓
式を1本化
↓
\(\frac{λ'}{λ}\)と\(\frac{λ}{λ'}\)の形を作る
↓
\(λ'=λ+Δλ\)とおき、近似
という流れで解いていきます。すると、最終的に連立式の解として
\(Δλ=\displaystyle\frac{h}{mc}(1-cosθ)[m]\)
\(Δλ=2.4×10^{-12}(1-cosθ)[m]\)
が求まります。過程が長くなるので、過程は別の項目にしておきます。
ここに書いた部分くらいまでは入試で必要な知識になってくるでしょう。
