[確認]運動方程式の立て方
斜面上に物体があったとしても、運動方程式を立てるときは、機械的に以下の手順で立てるのが楽です。
step1:力を作図
⇒まず重力を作図。そのあとで接触力をもれなく作図
step2:力の大きさを記入
step3:軸を設定し、軸に対して斜め向きの力は分解
step4:加速度の正の向きを設定
step5:記入した力に正負を記入
step6:物体ごとに立式

例題
図のように、傾きの角\(30°\)のなめらかな斜面上にある小物体(質量\(2.0kg\))を、斜面方向上向きに\(10.0N\)で引き上げた。このときの小物体の加速度の向きと大きさ\(a[m/s^2]\)を求めよ。重力加速度の大きさを\(9.8m/s^2\)とする。
[解答]
ステップに従って解いてみることにします。
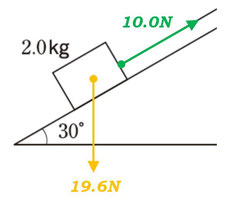
Step1:まず作図しましょう
物体が斜面上にあったとしても、重力は鉛直下向きに作図されます。
ここで重力の大きさは
\(W=mg\)
\(=2.0×9.8\)
\(=19.6N\)
となりますので、ついでに書き込んでしまいましょうか。

Step2:力の大きさを記入
重力を斜面方向と斜面に垂直な方向に分解します。
それぞれの大きさを求めて図中に書き入れますが、このとき、わざわざ\(sin\theta\)や\(cos\theta\)を考えなくても、三角形の比の関係から求められるのであれば、比から求めてしまいましょう。
ここでは、\(1:2:\sqrt{3}\)の関係から求めることができますので、斜面方向下向きへの重力の分力は、\(19.6N\)の半分の\(9.8N\)であるとわかります。
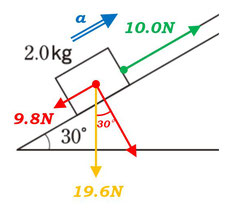
Step3:軸の設定
物体は斜面から浮いたり、斜面にめり込む可能性も、可能性で言えば否定はできないですが、普通に考えれば、どちらも起こりえず、おそらく斜面に沿って動くでしょう。この軸を運動の軸として考えます。
Step4:加速度の正の向きを設定
この問題では、おもりはどちらに動くでしょう。おそらく10人が10人とも、斜面に沿って上向きに進むと予想すると思います。なので、鉛直上向きを正としておきましょう。別に鉛直下向きを正にしてもかまいません。計算上の符号が逆になるだけで、最終解答は同じになります。

Step5:力の正の向きと負の向きを決める
斜面に沿って上向きを正としましたので、上向きに引き上げる力\(10.0N\)は、厳密には\(+10.0N\)という意味になります。重力の分力は斜面に沿って下向きにはたらく力ですので、\(-9.8N\)として考えます。
それぞれの力に「+」「-」を書きこめば十分ですが(もっと言えば「+」は省略できるので「-」だけ書けば十分ですが)、これも平地の問題と同様に、確実に点数になるまでは、図のように符号をマルで囲んでやって、強調しておくとミスは減ると思います。
Step6:立式する
ここまでやって、ようやく立式に進むことができます。
\(ma=F\) より
\(2.0×a=10.0-9.8\)
\(2.0a=0.2\)
\(a=0.1m/s^2\)
\(m\)は質量です。問題文に\(2.0kg\)と書いてあるので、それを代入しましょう。
\(a\)は加速度です。今求めたいのは加速度なので、ここに何かを代入することはありません。
\(F\)は合力で、作図したときに矢印の数だけ代入するものがあります。鉛直上向きに\(+10.0N\)、鉛直下向きに\(-9.8N\)の2本の矢印があるので、それらを右辺に代入します。
有効数字の計算の復習です。右辺で、\(10.0-9.8\)という計算処理をしていますが、「加減算は位を揃える」ルールですので、\(0.20\)ではありません。\(3\)ケタ-\(2\)ケタで\(2\)ケタ、とケタ数を揃えるのではなく、小数第一位をそろえて引き算をする、というルールの方が効いてきます。
その後の計算では、両辺を\(2.0\)で割る(\(2.0\)を移項すると考えても良い)、という計算をしています。左辺は\(2.0÷2.0=1.0\)という解釈で、有効数字が\(2\)ケタ分残っていると解釈してもいいですが、右辺は\(0.1÷2.0\)なので、「乗除算はケタ数を小さい方に揃える」ルールが適用されて、\(1\)ケタ割る\(2\)ケタで、\(1\)ケタとなります。よって、計算解答は\(0.1m/s^2\)です。\(0.10m/s^2\)ではありません。
鉛直上向きを正として、答えも「+」になりましたので、
向き:斜面に沿って上向きに
大きさ:\(0.1m/s^2\)
の加速度だということが分かりました。
今回は練習と気づきのために、有効数字の設定がややこしい問題を作りましたが、実際に問題を解くときには、こういう計算の細かい部分を気にしなくても解ける問題が多数ですので、有効数字が分からなくても、あまり気に病むことなく、問題の主軸の部分をしっかりつかむようにしておいてください。
ただ、有効数字の細かい部分の理解は、頭の片隅に常に置いておきたいですね。
