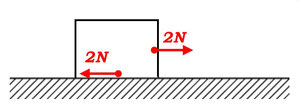
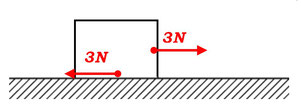
摩擦力
あらい面上に置かれた物体を面に平行に引いても、物体はすぐには動いてくれませんね。これは摩擦力が働いているからだということは、皆さんもすでに知っていることだと思います。
ですが、摩擦力は場合分けをすると実は\(3\)種類に分けることができて、それぞれ違う数式で説明されます。そこで、今まで知っているようで知らなかった摩擦力の細かい部分を、ここでは学んでいこうと思います。
静止摩擦力
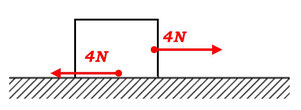
加える力を増やしても、物体が動かないときにはたらく摩擦力のことを「静止摩擦力」といいます。
物体は動きませんので、物体にはたらく力はつりあって、外力(外から加えた力)と静止摩擦力は常に同じ大きさになる、という関係があります。
▼静止摩擦力
加える力を\(F[N]\)、静止摩擦力を\(f[N]\)とすると
\(f=F\)
最大静止摩擦力
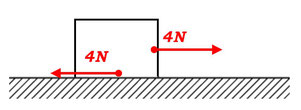
加える力を増やしていくと、物体はずっと動かないわけではなく、どこかで動き始める瞬間があるはずです。このとき、静止していられるための最大の摩擦力のことを「最大静止摩擦力」、もしくは省略して「最大摩擦力」といいます。
このときも物体は動きませんので、物体にはたらく力はつりあって、外力(外から加えた力)と静止摩擦力は常に同じ大きさになる、という関係があります。
ですが、この、動き始める瞬間の摩擦力の大きさのみ、物体や面の特性から計算ができます。物体が受ける垂直抗力を\(N[N]\)とすると、最大静止摩擦力は \(f_0=\mu N\) と表すことができます。ここで、\(\mu\)は面がどのくらいあらいかを表す数値で、「静止摩擦係数」といいます。係数なので単位はありません。
▼最大静止摩擦力
最大静止摩擦力を\(f_0[N]\)、垂直抗力を\(N[N]\)とすると
\(f_0=\mu_0 N\)
▼静止摩擦係数
面のあらさを表す数値
\(\mu\):静止摩擦係数(単位はない)
動摩擦力
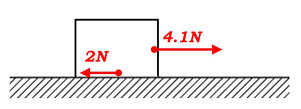
最大摩擦力をごくわずかに超える大きさで物体に力を加えると、ついに物体は動き出します。このとき、摩擦力の大きさは急激に小さくなって、物体はずいぶんと動かしやすくなるという特性があります。
物体が動いているときにはたらく摩擦力を「動摩擦力」といいます。
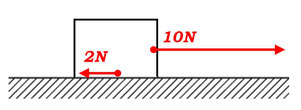
摩擦力が、一度動摩擦力に切り替わってしまえば、動摩擦力は物体の速さや加速度に関わらず、常に同じ値を示すようになります。
この動摩擦力の大きさも、最大静止摩擦力と同じように計算が可能で、次のように表されます。
▼動摩擦力
動摩擦力を\(f'[N]\)、垂直抗力を\(N[N]\)とすると
\(f'=\mu' N\)
▼動摩擦係数
面のあらさを表す数値
\(\mu’\):動摩擦係数(単位はない)
摩擦角
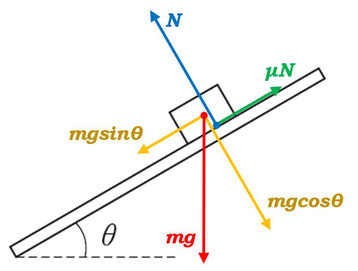
物体をあらい面上において、少しずつその面を持ち上げていきます。すると、どこかの傾きで物体は滑り出します。
このとき、滑らずにいられる最大の傾角のことを「摩擦角」といいます。摩擦角がどのように表されるのか、式で軽くたどってみましょう。
まずは重力\(mg\)を作図して、それを斜面方向と斜面に垂直な方向に分解します。
すると重力の分力は図の通り、それぞれ\(mgsin\theta\)と、\(mgcos\theta\)となります。
このとき、垂直抗力\(N\)は、重力の分力のうち、\(mgcos\theta\)の方とつり合いますので、
\(N\)\(=\)\(mgcos\theta\)
という関係式が得られます。
また、滑り始める瞬間の摩擦力は\(3\)つの摩擦力のうちの最大静止摩擦力を考えればいいので、\(f_0=\mu N\)の公式を持ってきましょう。物体がすべり始める瞬間を考えていますが、まだ静止しています。力はつりあいの関係にあるということを念頭においておきましょう。
最大静止摩擦力は、重力の分力のうち、\(mgsin\theta\)とつり合いますので、
\(\mu N\)\(=\)\(mgsin\theta\)
という関係式が得られます。ここに、垂直抗力を代入すると、
\(\mu\)\(mgcos\theta\)\(=\)\(mgsin\theta\)
\(\mu\)\(=\)\(\displaystyle\frac{mgsin\theta}{mgcos\theta}\)
\(\mu\)\(=\)\(tan\theta\)
となります。これが摩擦角の関係式です。
▼摩擦角
面を傾けたとき、物体がすべり出す瞬間の角度
\(\mu=tan\theta\)