空気抵抗
大気中を落下する物体は、大気から、運動の向きと逆向きの力をうけます。これを空気抵抗と呼びます。
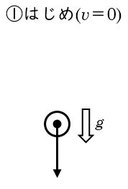
上空から雨滴が落下することを考えてみましょう。空気抵抗があってもなくても、最初は重力加速度\(g\)を受けて自由落下を行います。
例えば上空\(6000m\)から雨滴が落下したとします。仮に空気抵抗がなければ、自由落下の公式から計算すると、
\(v^2-v_0^2=2gy\) より
\(v^2=2×9.8×6000\)
\(v≒343m/s\)
となりますので、ほぼ音速ですね。雨の日に傘を忘れると、文字通り、だいぶ痛い思いをすると思います。
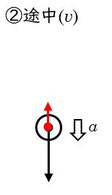
実際は空気抵抗がありますので、そうはなりませんよね。空気抵抗は、物体の速度が大きければ大きいほど、空気抵抗も大きくなる、という特性があります。
なので、落下途中の点では、重力の大きさは変わりませんが、空気抵抗が運動と逆向きにはたらき始めますので、重力加速度は\(9.8m/s^2\)より小さな値に変化していきます。
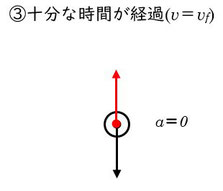
やがて、物体の速度が十分早くなると、空気抵抗がちょうど重力とつりあってしまって、もうそれ以上は加速しない大きさになります。加速度がゼロになると、加速も減速もしないということですから、物体の運動は等速になります。このときの物体の最終的な速度のことを「終端速度」と呼びます。
重力より空気抵抗が大きくなることはありません。仮にあったとすると、上向きの加速度が生じてしまいますので、それはやがて雨滴が上に落下することになってしまいます。今の設定では、空気抵抗は最大でも重力の大きさまでしか大きくなれません。
※初速度が終端速度より大きい場合は、はじめ、重力<空気抵抗となります。
粘性抵抗と慣性抵抗
空気抵抗には、物体の動く速さに応じて、粘性抵抗、慣性抵抗という2種類の抵抗が考えられます。
これらの抵抗は「流体力学」という分野で詳しく扱われるもので、空気に限らず、水流や油中の物体など、運動するときの抵抗であれば考慮するべきものですが、今回は空気抵抗を扱っていますので、「流体」というのが空気であるとして話を進めていきます。
▼粘性抵抗
比較的ゆっくり運動する物体にかかる抵抗を「粘性抵抗」といいます。入試で空気抵抗を扱った問題が出題されるときは、京大などの特例を除いて、ほぼすべて粘性抵抗が出題されますので、とりあえずのところは、これだけ押さえていれば十分です。(参考:2018京大Ⅰ)
比例定数を\(k\)として、
\(f=kv\)
で表します。
▼慣性抵抗
比較的速く運動する物体にかかる抵抗を「慣性抵抗」といいます。
比例定数を\(k\)として、
\(f=kv^2\)
で表します。
[補]係数\(k\)の概算
粘性抵抗の式は
\(f=kv\)
と表されますが、\(k\)の実際の中身を書いてみましょう。半径\(r\)の球について、ストークスの法則というものを書き出すと、
\(f=6\pi r \eta v\)
となります。ここで\(\eta[Pa・s]\)(イータ)は粘性率と呼ばれるもので、物体が運動している場所が空中なのか、水中なのか、はたまた油中なのかという、周囲にある「流体」のねばりの程度を表す量です。
それから、見ての通り、式中には\(r\)がありますので、物体の半径によっても当然ながら空気抵抗の大きさは変化します。
粘性率は\(20℃\)を常温とすると、空気で\(1.82×10^{-5}Pa・s\)、水で\(1.00×10^{-3}Pa・s\)、グリセリンなら、\(1.49×10^3Pa・s\)ほどの値になるそうですので、仮に質量\(145g\)、直径\(74mm\)(半径\(37mm\))の硬式野球ボールの、空気中での抵抗係数\(k\)を計算したとすると、
\(k=6 \pi r \eta\)
\(=6×3.14×3.7×10^{-2}×1.82×10^{-5}\)
\(=1.27×10^{-5}\)
となって、野球ボールには粘性抵抗はほぼ存在しないことがわかります。野球ボールの運動の場合は、速度が速いので、慣性抵抗の方が大きく効いているということですね。
一般に運動物体には、粘性抵抗も慣性抵抗も両方とも働きますが、通常、その2つの抵抗の大きさが大幅に違いますので、どちらかを無視して計算します。
じゃあ、どのくらいの速さで粘性抵抗と慣性抵抗が入れ替わるのでしょうか。そこから先は「流体力学」の世界ですので、大学に入ってから学びましょう。ベルヌーイの式やレイノルズ数、という言葉がこの分野を深追いしたときのキーワードです。
