変位
変位とは、位置の変化分のことを言います。
例えば、最初に数直線上の3mの位置にいたとして、ここから少し動いて5mの位置に移動したとします。このときの変位は2mです。また、最初に4mの位置にいたとして、移動して1mの位置に来たとすると、変位は-3mです。
このように、+や-も使って、移動した分だけの長さを表す量を「変位」と言います。
この「変位」を出すために途中式を書くとしたら、
「変位」=「移動後の位置」-「移動前の位置」
ということになりますね。これを高校物理では文字を使って、
\(Δx=x_2-x_1\)
と書きます。
\(Δx\)は「デルタエックス」と読み、「xの変化分」という意味を表します。
\(x_1\)が移動前の位置、\(x_2\)が移動後の位置ですので、最初と最後以外の途中の経路で、どんな寄り道をしたかは考えられていません。まっしぐらに進もうが、迂回しようが、ぐにゃぐにゃ進んだり、途中でUターンしても、最終的に\(x_2\)にたどり着けば、その差は\(x_2-x_1\)でいいんです。
実際に数字を入れて考えてもらう方が分かりやすいと思います。
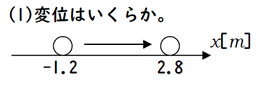
図を見てみましょう。単刀直入に聞きます。いくら移動していますか?
\(4m\)ですね。途中式を計算するのであれば、
\(2.8-(-1.2)=4.0\)
となります。このとき、「移動後の値-移動前の値」を計算していますが、これが変位を求める公式のようなものですね。
余談ですが、中学と違い、高校では、加減算をするときはケタを揃えます。なので、この問題の場合であれば\(4m\)ではなくて、\(4.0m\)と答えるよう癖づけておきましょう。詳細はまたいずれどこかで。
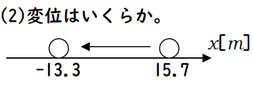
もう一問解いてみましょう。こちらであれば変位はいくらでしょう。答えを出すだけであれば簡単だと思います。
左向きに\(29m\)ですね。
これを物理の解答として完成させるには、「後-前」を計算して、
\(-13.3-15.7=-29.0\)
よって、変位は\(-29.0m\)です。
変位にはマイナスがつくこともあります。そして、小数点以下のゼロを忘れないことと、単位も忘れないこと。このあたりの細かいミスを減らす練習をしてくださいね。
移動距離
変位と似た用語に、「移動距離」、もしくは「道のり」、というものがあります。
変位は、その途中の経路がどれだけ曲がっていようと関係なく始点から終点までの直線距離を示します。これに対して「移動距離」は途中の経路全部の長さを考えなければいけません。
箱根駅伝では、往路107.5km、復路109.6kmで、往復217.1kmの「道のり(=移動距離)」を走破しますが、2日間かけて走っても始点と終点が同じですから「変位」はゼロですね。
