速度
物体の速さと向きを合わせた量のことを速度と言います。
北向きを正の向きとしたとき、北向きに\(12m/s\)の速さで走っている自動車がいれば、速度は\(+12m/s\)と表します。
また、南向きに\(15m/s\)の速さで走っている自動車がいれば、速度は\(-15m/s\)と表すことになります。\(+\)は省略して書いてもかまいません。
このように、一直線上の運動であれば、正負の符号を使って表すことが多いです。
そうではない場合は、言葉で表しましょう。例えば、北向きを正としているのに、東向きに速さ\(16m/s\)で走る自動車の速度を表さなければいけないときは、そのまま「東向きに\(16m/s\)」とすればいいわけです。たいがい、そういう問題のときには、どちらが正という風には指定されていないと思いますが、「速度」を表すためには「符号と大きさ」もしくは「向きと大きさ」のどちらかで表現すればいいので、どストレートに向きと大きさを丁寧に言葉で書いておけばまず間違いないでしょう。
これらを文字で表そうと思ったら、ある時刻からある時刻までの時間Δtの間に、ある位置からある位置までの変位Δxだけ移動するわけですので、「速度=距離÷時間」より
\(v=\displaystyle\frac{Δx}{Δt}\)
もしくはもっと正確に
\(v=\displaystyle\frac{x_2-x_1}{t_2-t_1}\)
と表します。\(x_1\)は移動前の位置、\(x_2\)は移動後の位置を表し、\(t_1\)は移動前の時刻、\(t_2\)は移動後の時刻を表しています。
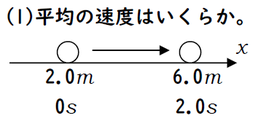
これも、文字だけではよくわからないので、実際に数字をあてはめながら考えてみましょう。
図を見てください。最初、時刻\(0s\)のときに、小球が数直線上の\(2.0m\)という位置にありました。これが移動して、時刻\(2.0s\)には\(6.0m\)の位置まで動いたとします。
このときの速度はいくらですか、ということですが、途中で加速したり減速したりしているかもしれませんので、ここでは言葉だけ「平均の」速度としています。解く上ではあまり気にしなくていいです。
さて、この速度ですが、\(2.0s\)間に\(4.0m\)だけ進んでいるのが分かりますね。なので、小学校以来の「距離÷時間」で速度が計算できます。
\(4.0÷2.0=2.0m/s\)
これが\(v=\displaystyle\frac{Δx}{Δt}\)
あるいは
\(v=\displaystyle\frac{x_2-x_1}{t_2-t_1}\)
の計算をしていることになります。
めちゃめちゃ難しく書かれているように見えますが、結局のところ「速さ×時間=距離」の関係さえ知っておけば、答えは出せるわけです。だからこの分野は公式を暗記する、とか、計算を正確にする、ということよりも、符号のミスがないか、単位を書き忘れていないか、「.0」を書き落としていないか、といったことの方がむしろ重点学習項目となります。
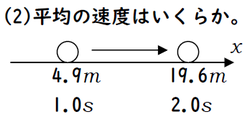
もう一問。これはどうでしょう。
\(1.0s\)間に\(14.7m\)進んでいますので、
\(14.7÷1.0=14.7m/s\)
ですね。
ただしこれを物理では、四捨五入して\(15m/s\)として、これを模範解答とします。
これは有効数字という物理特有の解答方法です。
\(14.7m\)のように、数字3ケタで表す物理量と、\(1.0s\)のように、数字2ケタで表す物理量を、かけ算したり割り算したりするときは、ケタ数の小さい方に合わせるというルールがあります。(補1 有効数字)
3ケタ÷2ケタの場合は、解答を2ケタにしなければいけないので、計算結果が\(14.7m/s\)のように3ケタになってしまった場合、四捨五入して2ケタに直してやる必要があります。
この有効数字の概念に飲み込まれてしまって、物理が苦手になる人が一定数いますが、よくわからなければいっそ無視してしまってもいいと思います。一つ一つを習った順に完璧に仕上げながら学習するよりも、ざっくり全体を見渡す力をつけてから、最後に細かい部分を詰めていくのも方法としてはありでしょう。
