(1)
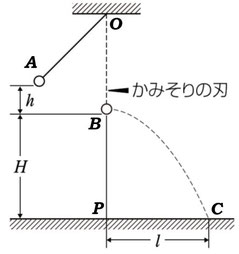
小球の質量をm、点Bの高さを位置エネルギーの基準面とする。
点Aと点Bとの間での力学的エネルギー保存則より
\(mgh=\displaystyle\frac{1}{2}mv_0^2\)
\(×\frac{2}{m}\)
\(2gh=v_0^2\)
\(v_0=\sqrt{2gh}\)
(2)
点Bから点Cの運動は水平投射です。高さHを落下するのにかかる時間は自由落下にかかる時間と同じなので、
\(H=\displaystyle\frac{1}{2}gt^2\)
\(t^2=\displaystyle\frac{2H}{g}\)
\(t=\sqrt{\displaystyle\frac{2H}{g}}\)
この間、水平方向に進む距離は、等速直線運動の公式から、
\(l=v_0t\) より
\(l=\sqrt{2gh}・\sqrt{\displaystyle\frac{2H}{g}}\)
\(l=2\sqrt{hH}\)
(3)
点Cの高さを位置エネルギーの基準面に取り直して、点Bと点Cとの間での力学的エネルギー保存則より、
\(mgH+\displaystyle\frac{1}{2}mv_0^2=\frac{1}{2}mv^2\)
\(×\frac{2}{m}\)
\(2gH+v_0^2=v^2\)
\(v_0=\sqrt{2gh}\)を代入
\(v^2=2gH+2gh\)
\(v=\sqrt{2g(H+h)}\)
もしくは、点Aと点Cとの間での力学的エネルギー保存則より、
\(mg(H+h)=\frac{1}{2}mv^2\)
\(×\frac{2}{m}\)
\(2g(H+h)=v^2\)
\(v=\sqrt{2g(H+h)}\)
で求めてもいいですね。
