物基39　縦波と横波

　波にはいろいろな種類のものがあります。高校で主に扱うのは横波と縦波、そしてごくごくたまに水面波や表面波という特殊な波が扱われます。

　波が進む向きと振動する向きが垂直なものを横波、波が進む向きと振動する向きが水平なものを縦波といいます。

▼縦波と横波

縦波　進行方向と振動方向が垂直

　例：音波、地震波のP波

横波　進行方向と振動方向が水平

　例：光波、地震波のS波

　※３つ目の図をクリックすると拡大します。パソコンから見る人は図が小さいので、拡大してください。

　上の縦波のgif画像を見てください。波は時間とともに右に進行していますが、媒質のそれぞれの棒はある場所を中心に左右に振動しています。

　横波の場合は振幅や波長を決めるのが簡単そうに見えますが、縦波の場合は横波と同じ方法では求められなさそうです。なので、波の種類によって解き方を変える必要がありそうですね。ですが、縦波を横波のようにグラフ化して考える方法が編み出されています。縦波が横波のように書かれていれば振幅も波長も簡単に求められそうです。

　３つ目の図を見てください。１段目は振動する前の様子、２段目は振動している、ある瞬間の縦波の様子、３段目は縦波を横波のように描こうとしている図の一部を表しています。

　点１’は初めの位置から少し左に移動しています。このズレを変位と言いますが、変位をx軸基準で見てやると、左にズレるということはマイナスにズレるという意味になります。このx軸へのズレをy軸へのズレと解釈して、ズレた分だけy軸に点を取ってやります。例えばここで、点１’が、元の点より3cmだけ左側、つまり－3cmだけ変位しているとします。点２’は0cmの変位、点３’は＋3cmの変位、点４’は＋5cmの変位、のように元の位置からどのくらい左右に変位しているのかを表にしたとします。

　ここでの数字は、例えばという値なので深く考えずに読み進めてください。

▼媒質のズレ 

　この、本来はx軸のズレで説明されるものをすべてy軸の値として読み替えることにします。そして点を取っていき、なめらかにつなぐと、横波と同じような形で表すことができます。

　これを縦波の横波表示といいます。こうすることで、振幅A[m]や波長λ[m]だけでなく、横波で使っていた公式すべてを縦波でも利用することが出来るようになりました。

(1)

　点10’の左右のズレを見てみましょう。横波表示した点9'の座標は負です。y軸の変位は本来はx軸のズレを意味していますので、x軸の負、つまり左にズレていることを意味します。

　点11’は正のズレ、つまり右にズレていることを意味しますので、その真ん中にある点10’は左右へ引っ張られていることになります。

　よって、点10’のような右上がりの交点は縦波の疎を表します。

(2)

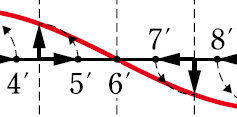
　点6’の左右のズレも見てみましょう。今度は点5’が正の変位、つまり右にズレていて、点7’が負の変位、つまり左にズレているので、真ん中の点6’は左右から押しつぶされていることになります。

　よって、点6’のような右下がりの交点は縦波の密を表します。