Kundt(クント)の実験(1866)として知られている気柱の共鳴実験です。
空気の振動柱となっている筒内に微小な粉末を入れると、共鳴の定常波の腹、もしくは節に粉末が集まる特性があります。
封入する粉末がスチロールなどの大きい粒である場合、粉末は腹の位置に集まります。
封入する粉末が霧や石松子(せきしょうし)などの微粒子である場合は、節の位置に集まります。
[新潟県の 笹川先生の論文]
クントの実験における粒子の運動(外部リンク)
J-stageのページに進んで、pdfをダウンロードすると読むことができます。
問1
気柱の右端のふたが固定端、振動板は振動するため自由端、その間に粉の集まりが(振動板付近のものも含めて)3か所あるので、振動が5倍振動になっていることが読み取れます。
また、解答には影響がありませんが、粉末は振動の腹の位置に集まっていると読み取れるので、スチロール粉末など比較的大きめの粒子で実験を行っているようですね。
(あ)
\(λ_A=\displaystyle\frac{4}{5}l_A\)
(い)
\(V_A=fλ_A\) より
\(V_A=\displaystyle\frac{4}{5}l_Af\)
(う)
\(f\)が5倍振動なので、この気柱が共鳴を起こす最も低い振動数(基本振動)は、\(f\)の\(\displaystyle\frac{1}{5}\)である。
よって、\(f_0=\displaystyle\frac{1}{5}f\)
(え)(お)
音波は縦波であるので、筒領域Ⅰにある空気柱が、密度を変えながら左右に振動していると考えられる。
図の状態から少しだけ時間が経過すると、筒領域Ⅰがいくらかの変位分だけ動くというわけである。
このときの変位分を、筒領域Ⅰの左側の壁と右側の壁とを別々に考えると、筒領域Ⅱを求めることができる。
筒領域Ⅰの左側の壁は、位置\(x\)にあったものが変位\(y\)、つまり位置\(x+y\)に移動する。
右側の壁は、位置\(x+Δx\)にあったものが変位\(y+Δy\)、つまり位置\(x+y+Δx+Δy\)に移動する。
筒領域Ⅱとは、左側の壁が\(_{(え)} x+y\)、右側の壁が\(_{(お)} x+y+Δx+Δy\)にあるような空気中のことをしめす。
(か)
筒領域内にある気体の質量を\(m\)とすると、\(m\)はⅠとⅡで同じ値である。
\(m=ρV\) より
\(m=ρ_ⅠV_Ⅰ\)
\(m=ρ_ⅡV_Ⅱ\)
よって
\(ρ_ⅠV_Ⅰ=ρ_ⅡV_Ⅱ\)
\(\displaystyle\frac{ρ_Ⅱ}{ρ_Ⅰ}=\frac{V_Ⅰ}{V_Ⅱ}\)
\(V=Sl\) より、底面積は変わらないので、長さだけで考えればよい
\(\displaystyle\frac{ρ_Ⅱ}{ρ_Ⅰ}=\frac{Δx}{Δx+Δy}=\frac{1}{1+\frac{Δy}{Δx}}\)
(き)
\(\displaystyle\frac{ρ_Ⅱ}{ρ_Ⅰ}\)が最小になるためには\(\displaystyle\frac{Δy}{Δx}\)が最大となればいいので、③
問2
閉管における5倍振動のグラフを描くのは難しくないが、この問題で問われている形に表現するのはミスが出やすいかもしれない。通常、閉管における共鳴の様子を図示するときは、いわゆる「葉っぱ型」で描いたものをよく目にする。

この問題では、「ある時刻における」疎密を記入するように指示されているので、「ある時刻」は自分で決めてよいと思われる。つまり、上図のどちらの波を描いてもいいので、解答者が選んだ好みの波形での疎密を考える。
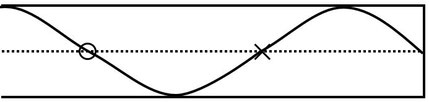

おそらく、想定されている解答は上のような2図であろう。しかし、「ある時刻における」図を用いて描くようにとしか指示されていないので、本校の物理科教員内では、

こういうものも含めれば無限に解答の種類を作れるよね、という話になった。要は疎密がわずかにでも現れれば解答が可能であるから、グラフが直線になる一瞬を除いて、好きな図を書けばよさそうである。
もちろん、グラフは縦波である音波を表しているので、疎(×)が上り坂の交点、密(○)が下り坂の交点であることは間違えない前提での話である。
(く)
5倍振動の次に共鳴するのは7倍振動であるから、
\(λ_B=\displaystyle\frac{4}{7}l_B\)
(け)
図1より前にあるリード文まで戻る。最初のパラグラフ3行目に「容器内の気圧が外気圧と等しくなる」ことが書かれている。
問2の下にある文章のように、「この容器内の空気を上げていくと、容器のふたが水平方向に動いて」いるが、この間、気柱内の気圧は外気圧と等しいままである。わずかにでも違いがあれば温度を変えなくとも、気圧が大きい方から小さい方へと、ふたが動いてしまう。
気圧が一定なので、Charles(シャルル)則より
\(\displaystyle\frac{V_A}{T_A}=\frac{V_B}{T_B}\)
\(V=Sl\) より、断面積は同じであるから
\(\displaystyle\frac{l_A}{T_A}=\frac{l_B}{T_B}\)
よって
\(T_B=\displaystyle\frac{l_B}{l_A}T_A\)
(こ)
5倍振動と7倍振動との比であるから、
\(\displaystyle\frac{7}{5}\)
\(λ_A=λ_B\)とおいて、
(あ)と(く)をそれぞれ変形して\(\displaystyle\frac{l_B}{l_A}\)に代入しても求まる。
(さ)
\(T_B=\displaystyle\frac{l_B}{l_A}T_A\) に対して、(こ)を代入すると、
\(T_B=\displaystyle\frac{7}{5}T_A\)
(し)
\(l_A=\displaystyle\frac{5}{4}λ_A\)
\(l_B=\displaystyle\frac{7}{4}λ_B\)
より
\(\displaystyle\frac{l_B}{l_A}=\frac{7λ_B}{5λ_A}\)
\(\displaystyle\frac{l_B}{l_A}=\frac{7\frac{V_B}{f}}{5\frac{V_A}{f}}\)
\(\displaystyle\frac{l_B}{l_A}=\frac{7V_B}{5V_A}\)
音速が一定なら\(V_B=V_A\)であるから、
\(\displaystyle\frac{l_B}{l_A}=\frac{7}{5}\)
であるが、いま音速が\(V_B>V_A\)であるから、元の値よりは大きい値になる。
よって①
問3
音速 \(V=V_0+bT\) より
\(V_A=V_0+bT_A=fλ_A=\displaystyle\frac{4}{5}fl_A\) ---①
\(V_B=V_0+bT_B=fλ_B=\displaystyle\frac{4}{7}fl_B\) ---②
この連立式を解くだけでいいわけだが、式変形がなかなかつらい。
②式
\(V_0+bT_B=\displaystyle\frac{4}{7}fl_B\)
に、(け)式 \(T_B=\displaystyle\frac{l_B}{l_A}T_A\) を代入すると
\(V_0+b\displaystyle\frac{l_B}{l_A}T_A=\frac{4}{7}fl_B\) ---③
①式より
\(V_0=\displaystyle\frac{4}{5}fl_A-bT_A\)
これを③式へ代入すると
\(\displaystyle\frac{4}{5}fl_A-bT_A+b\frac{l_B}{l_A}T_A=\frac{4}{7}fl_B\)
\(\displaystyle(\frac{l_B}{l_A}-1)bT_A=(\frac{4}{7}l_B-\frac{4}{5}l_A)f\)
\(\displaystyle\frac{l_B-l_A}{l_A}bT_A=\frac{4}{35}(5l_B-7l_A)f\)
\(b=\displaystyle\frac{4(5l_B-7l_A)fl_A}{35(l_B-l_A)T_A}\)
ここまでで、まず連立式の解答の1つが求まりました。
あとは代入して残りの未知数を求めればいいですね。
③式へ代入すると、
\(V_0=\displaystyle\frac{4}{5}fl_A-\frac{4(5l_B-7l_A)}{35(l_B-l_A)}fl_A\)
\(V_0=\displaystyle\frac{28(l_B-l_A)-4(5l_B-7l_A)}{35(l_B-l_A)}fl_A\)
\(V_0=\displaystyle\frac{28l_B-28l_A-20l_B+28l_A}{35(l_B-l_A)}fl_A\)
\(V_0=\displaystyle\frac{8l_B}{35(l_B-l_A)}fl_A\)
よって
\(V_0=\displaystyle\frac{8fl_Al_B}{35(l_B-l_A)}\)
