川を渡る向きの速度は、川を渡る時間と関係があり、川を流れる向きの速度は、川を渡る時間とは無関係であることに注意をしましょう。
例えば、最初に船がいる場所を原点として、川の流れる向きをx軸、川を渡る向きをy軸として、グラフ上を船が動くことを考えてみます。川を渡り切るためには、y座標がいくらかの値をもつところまでたどり着けばいいですが、川の流れが速かろうと遅かろうと、川の流れによって変化するのはx座標の値ですね。
なので、「川を渡る」ためにはy軸のことだけ考える必要があり、「川を流される」ためにはx軸のことだけ考える必要があります。物理はこんなふうにして、軸の独立というとらえ方をします。
(1)
向こう側の岸へ到着するまでの時間を最短とするには、川が流れていようと流れていまいと、川の流速は川を渡る時間とは関係しないので、単純に船の舳先(へさき)を川の流れに垂直にすればいいですね。
よって θ=90°
また、渡り切るためにかかる時間は、川幅が72mなので、川の流れに垂直な向きに2.0m/sで進むのであれば、速さ・時間・距離の関係から、距離÷速さ より
72÷2.0=36s
このとき、川の流れによって流されているので、最短時間で到着してはいますが、船が実際に進んだ距離が最短距離(72m)ではないことに気をつけてください。実際には、流速1.2m/sで36s間だけ流されて、43.2mだけ下流の対岸に到着しています。
(2)
船の舳先(へさき)を60°の向きに向けて進むとき、川が流れる向きと、川を渡る向きとにそれぞれ速度の成分を分解すると、図のようになります。
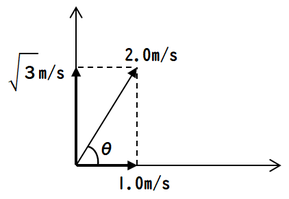
ここに、さらに川の流速1.2m/sが加えられるので、実際の船の速度は次の図のようになります。

この赤い太矢印で表されている速度を、三平方の定理で計算すると、
\(v^2=2.2^2+\sqrt{3}^2\)
\(v^2=4.84+3\)
\(v=\sqrt{7.84}\)
このルートは単純には外せません。
そこでルートの中身について、素因数分解を行い、
\(0.1)\underline{7.84}\)
\(0.1)\underline{78.4}\)
\(2)\underline{784}\)
\(2)\underline{392}\)
\(2)\underline{196}\)
\(2)\underline{98}\)
\(7)\underline{49}\)
(素因数分解ってどうやったら表示崩さずに書けるんだろうか…)
\(v=\sqrt{0.1×0.1×2×2×2×2×7×7}\)
\(v=0.1×2×2×7\)
\(v=2.8m/s\)
また、川を渡るのに要する時間は(1)と同様に、川の流れに垂直な向きへの速度成分を用いて、
距離÷速さ より
\(t_2=72÷\sqrt{3}\)
\(t_2=\displaystyle\frac{72}{\sqrt{3}}\)
\(t_2=\displaystyle\frac{72\sqrt{3}}{3}\)
\(t_2=24\sqrt{3}\)
\(t_2=24×1.73\)
\(t_2=42s\)
