問題文に与えられている図が、図1は加速度の図、図2は速度の図、という風に統一されていないので、ただでさえ難しそうな問題が、さらにややこしくなっていますね。
いったんどちらの図も速度の図に統一してしまいましょう。
加速度・速度・距離の分野の問題が出題されたときは、速度のグラフが最も便利です。
速度グラフがあれば、傾きから加速度、面積から距離を求めることができるので、1つのグラフで大体の情報は網羅できます。
速度グラフが与えられていないときや、グラフそのものが与えられておらず、文章だけで書かれているときは積極的に速度グラフを書いてみるといいかもしれませんね。
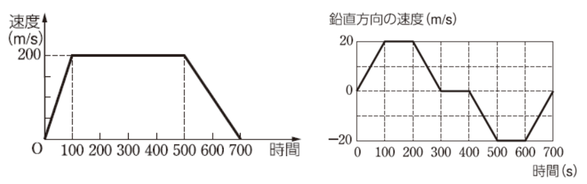
図1のつくり方を確認しておきます。
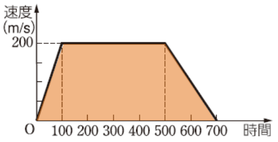
\(0~100s\)は、加速度が\(2.0m/s^2\)ですので、速度グラフでは傾き\(2.0\)のグラフとします。\(100s\)後には\(200m/s\)となりますね。
そこから\(100~500s\)間は加速度0なので、速度は等速。\(500~700s\)間では加速度\(-1m/s^2\)なので、速度グラフでは傾き\(-1\)で減少し、ちょうど速度0でグラフが終わりますね。
あ、書き忘れましたが、左の図が「図1」で、「水平方向の速度グラフ」です。
右の図が「図2」で、「鉛直方向の速度グラフ」です。
このグラフ作成は、書かなければ正解までもっていけない、というほどの作業ではありませんが、断然ラクになるので、リードの模範解答と同様に、いったん作成しておきます。
リードの解答にはきちんと別解も示してありますので、グラフが描けないひとは、そちらを見てもいいかもしれません。
(1)
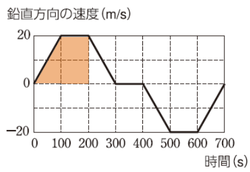
離陸してからの高度は、鉛直方向のグラフにおける面積から求めます。
台形の面積公式
(上底+下底)×高さ÷2
を用いると、
\(\displaystyle\frac{1}{2}(100+200)×20=3000\)
問題文には、kmで答えることが求められているので、
\(3.0km\)
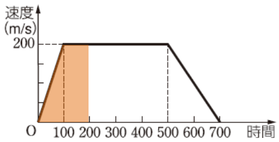
同様に、水平距離は、
\(\displaystyle\frac{1}{2}(100+200)×200=30000\)
問題文には、kmで答えることが求められているので、
\(30km\)
(2)
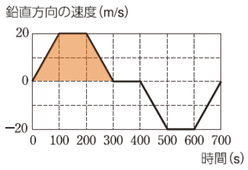
飛行中の最大高度は、鉛直方向の速度グラフで速度が初めて0となる300sまでのグラフの面積を求めれば求まりそうです。
\(\displaystyle\frac{1}{2}(100+300)×20=4000\)
よって
\(4.0km\)
(3)
SL間の水平距離はグラフ全部の面積から求めます。
\(\displaystyle\frac{1}{2}(400+700)×200=110000\)
よって
\(110km=1.1×10^2km\)
(4)
飛行機が最大高度に達したとき、というのは、(2)から、\(300s\)の時点だということが分かっています。
このとき、「この飛行機」の速さは、\(200m/s\)なので、\(0.2km/s\)ですね。
一方で、「別の飛行機」の速さは、ずいぶん速くて、\(1.7km/s\)なので、接近する速度は、
\(1.7km/s-0.2km/s=1.5km/s\)
となります。
