波の独立性
粘土の塊が2つあったとします。この粘土の塊2つをぶつけた瞬間の様子をスローモーションで撮影しているイメージをしてみましょう。粘土がぶつかっていくごとに、少しずつ形が変わっていき、やがて一体化して実験が終了します。
大きさの違う鉄球2つで同じ実験をするとどうでしょう。2球は変形することなくゆっくり衝突し、衝突後はそれぞれ反対方向に動きくでしょう。
このように、力学では、ある物体と別の物体が衝突すると、一体化したり、反発したりします。
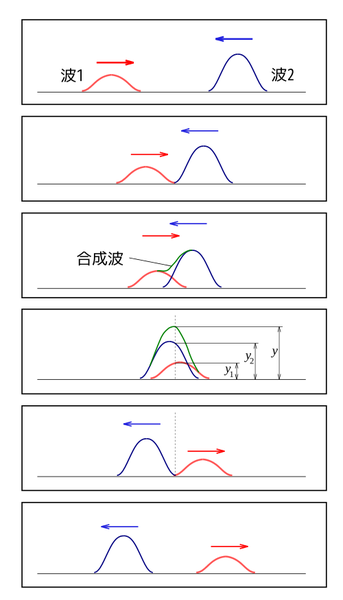
波の場合で同じように左右から衝突させてみましょう。
衝突してすぐのときは、力学のように形が徐々に変化しています。ところが波の場合は力学と違い、このまま2つの波は素通りしてしまいます。
波1と波2が同じ波であれば、もしかしたら力学でいう鉄球の衝突のように、2つの波が衝突後にはね返っていくように見えるかもしれません。
ですが、それぞれの波は相手の波がまるで存在しなかったかのように、素通りしていき、形は元の状態を保ったままです。
このように、波の衝突前後で、波の形状も速さも変わらず、相手の波の進行を一切妨げることなく、そのまま進行し続けるような性質を波の独立性といいます。
波の重ね合わせ
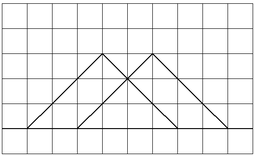
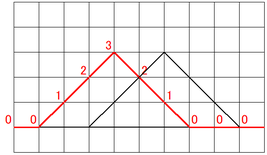
波が衝突した瞬間の様子を作図してみましょう。
図のような波があったとします。この2つの波がぶつかったときの様子を作図します。このような操作を波の重ね合わせと言います。
波を作図するときは、縦軸の座標だけを足し合わせます。
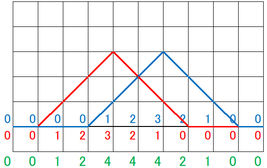
初めから、それぞれの高さを並べて書くと見やすかったですね。
赤で示した左側の波の高さと、青で示した右側の波の高さを、それぞれ単純に足し合わせます。
一番右端の0を書き忘れてました。図を直すのはめんどくさいので、ここでひっそりと書き足しときますね。どこのことかわかりますよね。
この図、Excelで作ってるんですが、いちいち線引いたり色付けたり、スクリーンショット取って画像化して切り抜いて貼って…、まぁ直すのがめんどくさいんです。許して。
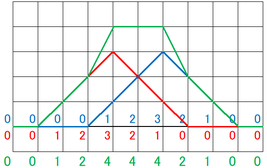
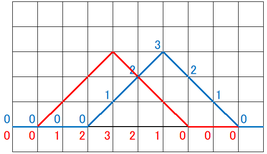
そして最後に、足し合わせた緑の数字をもとに、それぞれのマス目に足し合わせた高さを記録していき、線でつないでやります。
このように、緑で示したような波形が、重ね合わせをしたあとの波で、合成波と言います。
波の重ね合わせをするときは、このように各点各点の高さを記録して、それぞれを足し合わせる操作を繰り返しているだけです。
注意を要することが2点あります。まず1点目は、高さにはマイナスが出てくることもある、ということです。
厳密に言えば、ここで足し合わせている値は「y座標の値」です。単なる座標値ですから、正の値に限定しているとは限りません。
もう1点は、足し合わせる波形は三角波や矩形波(長方形の波)のように、カクカクした波だけとは限らない、ということです。正弦波(サインカーブ)のように、なめらかな曲線型の波形を足し合わせる場合は、マス目とマス目の間に波がどのくらいの高さで存在しているのかを目分量で数えます。(0.8マスとか、1.4マスのように)
そして、同様に足し合わせてやると合成波が描けます。
ここの分野は、合成波が描けるかどうか、ということよりも、短時間で素早く処理できるかどうか、の方が重要性は高いかもしれません。丁寧に読めば読むほど合成波はきれいに厳密に描くことができますが、テストの制限時間のことも考えると、見切りをつけるべき部分もありますから、練習量を積みましょう。