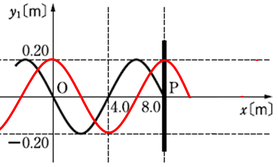
(1)
波の速さは2.0m/sなので、1.0s後には波は2.0mだけ右に進みます。
進行している波は連続波なので、問題の図に記載されている部分の波だけでなく、左側に永遠に続いている波も考えて作図してください。
図の左端めいっぱいまで波を描きます。
これによって、
点Pの入射波の変位(縦軸座標)は、0.20m
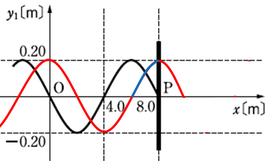
次に、壁の内側に描いた仮想的な波を折り返します。
いま、自由端を考えているので、線対称に折り返します。
線対称に折り返す際、壁の内側の波を消してはいけません。作図に用いた線はすべて残しておきましょう。
これによって、
点Pでの反射波の変位も0.20m
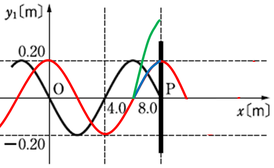
合成波は、入射波の変位と反射波の変位を足し合わせてやればいいので、
0.20+0.20=0.40m
となります。
作図すると、図の緑色の波形の部分が合成波の部分です。
(2)
おそらく、ほとんどの人がまず作図をして考えていくと思いますが、作図をせずに解く方が早いので、そちらの方法を教えます。
腹や節の位置、と問われた場合、この問題は定常波の問題です。
定常波の特徴として、振幅こそ元の波の2倍になりますが、振動数も波長も周期も、元の波と同じ値を取ります。
つまり、節は何個か、という問いに対して即座に判断できることとして、節と節の間の距離は元の波での交点と交点との距離と同じ、というワザが使えます。
この問題の場合だと節間隔は4.0mですね。
次に、固定端反射の問題だということから、少なくとも点Pは固定されているため節そのものになる、ということが分かります。
あとは、ここを起点に4.0mごとに節があるわけですから、x=8.0、4.0、0mの点に節があるということがわかり、節の数は3個と判断できます。
(3)♦
定常波の腹の振幅は、元の波どうしの重ね合わせなので、振幅が2倍になります。
よって、0.20×2=0.40m
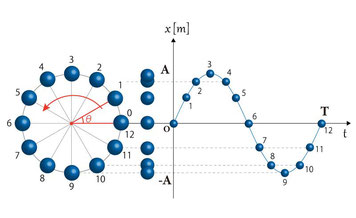
次に、節と腹の中点における振幅がいくらか、という問いに対してですが、ここでは(物理基礎では)少し特殊な解き方をします。
定常波の波の変位が、円運動している物体の縦座標の変位としても表せる、という考え方を利用します。波形の3の変位は円でいう90°のy座標の値、波形の6の変位は円でいう180°のy座標の値、という風に換算します。
そうすると、一見中途半端な波形の1のような変位でも、円に換算すると30°のy座標だからsin30°なりを使えば求めることができるぞ!となるわけです。
この問題では、腹の振幅が0.40mなので、円の半径は0.40mとして考えます。
波形を見る限りでは、節と腹の中点というのは図でいうところの1と2の間あたりですので、具体的に振幅(縦座標)がいくら、というのは波の図からは読めません。
ところが、円で相当させると、ちょうど45°の高さに相当するので、
\(y=0.40×sin45°\)
\(y=0.40×\displaystyle\frac{\sqrt{2}}{2}\)
\(y=0.20\sqrt{2}\)
\(y=0.20×1.41\)
\(y=0.28[m]\)
と求めることができます。
