■解答
(イ) \(-V\) (ロ) \(I\)
(ハ) \(\displaystyle\frac{\pi}{2}\) (ニ)\(\displaystyle\frac{Q_0}{\sqrt{LC}}\)
(ホ) \(\displaystyle\frac{E}{r}\) (ヘ)\(-V'\)
(ト) \(I\) (チ)\(\displaystyle\frac{\pi}{2}\sqrt{LC}\)
問1
\(V=E+I_0\sqrt{\displaystyle\frac{L}{C}}\)
(リ) \(E\) (ヌ) \(-\displaystyle\frac{V}{R}\)
(ル) \(E-V\) (ヲ) \(I-\displaystyle\frac{V}{R}\)
問2
\(V_0=E+\alpha t = (1+\alpha)E\)
\(I_0=(1+\alpha)^2\displaystyle\frac{E}{R}\)
問3
\((\alpha+1)^2\)倍
■解説
(イ) 公式どおりです。誘導起電力は、電流の変化ΔIについて、逆符号の電圧を生じるので、
\(L\displaystyle\frac{ΔI}{Δt}=-V\)
\(ΔI\)の符号次第で電圧の正負も入れ替わります。
(ロ) 既知の公式からでも作れますが、問題文にあるものを活用していきましょう。
\(ΔQ=CΔV\) と \(ΔQ=IΔt\) が成立するので、
\(CΔV=IΔt\)
よって
\(C\displaystyle\frac{ΔV}{Δt}=\frac{IΔt}{Δt}=I\)
(ハ)
\(\displaystyle\frac{π}{2}\)だけ位相が遅れます。
コンデンサーの電流電圧関係は、電流のピークが先に来て、電圧のピークが後に来ます。
コイルの電流電圧関係では、逆に電流のピークが後に来て、電圧のピークが先に来ます。
これらを簡単に表せるメモ書きとして、「CIVIL」を活用しましょう。
Cは、Iが来て→Vが遅れる、Vが来て→Iが遅れるのがL
と表しているのが「CIVIL」というわけです。
単に\(\displaystyle\frac{π}{2}\)進む、遅れる、とだけ暗記してしまうと、VのIに対するズレなのか、IのVに対するズレなのか分からなくなります。
Cは、Iが来てVが遅れるので、VはIに対して、つまりVはIから見て、\(\displaystyle\frac{π}{2}\)遅れているわけです。
(二) 交流理論から解く方法と、エネルギー保存則から解く方法があります。これは力学でもおなじみの別解探索ですね。時間的に追跡するか、保存則を探すか、という2パターンは常に意識しておきましょう。
①交流理論から解く
\(V=V_0sinωt\) とすると
\(I=C\displaystyle\frac{ΔV}{Δt}\)
\(=C\displaystyle\frac{V_0Δsinωt}{Δt}\)
ここで数Ⅲ公式、\(\displaystyle\frac{Δsinωt}{Δt}=ωcosωt\) より
\(I=CV_0ωcosωt\)
\(I=Q_0ωcosωt\)
これは(ハ)の根拠となる式ですから、きちんと\(\frac{π}{2}\)の遅れがあることも読み取れます。
ここから最大値を求めると、cosωtの最大値は三角比のルールとしてどんなωtを取っても1ですので、
\(I_{max}=Q_0ω\)
\(ωL=\displaystyle\frac{1}{ωC}\)
\(ω^2=\displaystyle\frac{1}{LC}\)
\(ω=\displaystyle\frac{1}{\sqrt{LC}}\) より
\(I_{max}=\displaystyle\frac{Q_0}{\sqrt{LC}}\)
②エネルギー保存則から解く
こっちの方が簡単です。
\(\displaystyle\frac{1}{2}CV_0^2=\frac{1}{2}LI_0^2\)
\(I_0^2=\displaystyle\frac{C}{L}V_0^2\)
\(I_0=V_0\displaystyle\sqrt{\frac{C}{L}}\)
ここに\(Q_0=CV_0\)を入れ込んで、
\(I_0=\displaystyle\frac{Q_0}{C}\sqrt{\frac{C}{L}}\)
\(I_0=\displaystyle\frac{Q_0}{\sqrt{LC}}\)
(ホ)
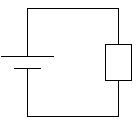
図2において、十分長い時間が経過すると、回路の右側部分はコンデンサーが満充電され断線状態になり、回路の左側部分はコイルによる誘導効果がなくなってコイルは導線としてみなせます。
結果として、電源電圧\(E\)で、抵抗\(r\)に電流\(I\)が流れている回路が残っています。
キルヒホッフの法則より
\(E=rI\) なので、
\(I=\displaystyle\frac{E}{r}\)
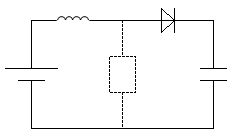
(ヘ)
コンデンサーの両端に現れる電圧\(V\)の\(E\)からの変化分を\(V'=V-E\)と置いているので、コンデンサーの両端の電圧は\(V=E+V'\)と表せます。
符号に悩むかもしれませんが、問題文をそのまま追いかければいいですよ。なぜ\(E+V'\)と書くのか、問題文をたどってみます。
そもそもスイッチを閉じて十分時間がたっていますので、コンデンサーは初期状態で満充電の状態です。当然、電圧は\(E\)です。
ここからスイッチを切ると、問題文には「ダイオードに電流が流れ、コンデンサーが充電される」と書いてあります。つまり、コンデンサーは電源電圧\(E\)を超えて充電することが出来るということが読み取れます。
しかも、電圧の変化分\(V'\)は正となるわけですから、文字式の中身に負が隠れているわけでもないですね。
ダイオードは理想的な整流作用をもつとしますので、ここでは導線と同様のものと考えましょう。
京大の過去問の中には、ダイオードの整流作用を厳密に考える問題と、理想的に考える問題とがありますので、無条件に導線と読み替えずに本文中の根拠を必ずチェックしておきましょう。
さあようやく本題です。
キルヒホッフの法則より
\(E+(-L\displaystyle\frac{ΔI}{Δt})=E+V'\)
よって
\(L\displaystyle\frac{ΔI}{Δt}=-V'\)
長々と書きましたが、解答部分は2行だけでおしまいです。
(ト)
また、電気量が\(ΔQ=IΔt\)だけ流入したとき、コンデンサーの電圧が\(ΔQ=CΔV'\)の関係で微小変化することから、
\(CΔV'=IΔt\)
よって
\(C\displaystyle\frac{ΔV'}{Δt}=I\)
(へ)と(ト)に関する符号の検算をしておきます。問題文より「\(V'\)は正となり、\(I\)は減少し始める」ので、\(ΔV'>0\)と\(ΔI<0\)から、(ト)\(>0\)と(へ)\(<0\)が容易に確かめられます。
(チ)
電流の時間変化は、\(I=I_0\)から\(cos\)カーブを描いて減少していくので、はじめて\(I=0\)となる\(\frac{T}{4}\)の値を求めればいいですね。
振動が続いたとすると、前問から\(T=2\pi\sqrt{LC}\)の周期で振動しますが、いま、ダイオードが存在するため、\(I\)が負にならないので、振動は\(\frac{T}{4}\)で停止します。
\(T_1=\displaystyle\frac{T}{4}\)
\(T_1=\displaystyle\frac{1}{4}・2\pi\sqrt{LC}\)
\(T_1=\displaystyle\frac{π}{2}\sqrt{LC}\)
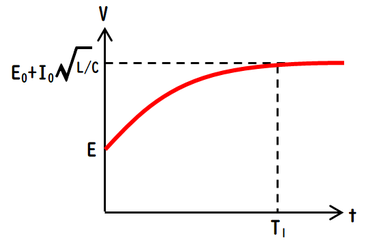
問1
最初の電位\(E\)から指数関数的に上昇して、時刻\(T_1\)に、ある電位\(V\)となるようなグラフになります。ここまでは秒殺ですが、最終的に行き着く\(V\)の具体的な中身を求めるために一苦労が必要です。
コイルに蓄えられていた最初のエネルギーは
\(\displaystyle\frac{1}{2}LI_0^2=\frac{1}{2}L(\frac{E}{r})^2\)
\(Q=CV'=C(V-E)\) より
電源から供給されるエネルギーは
\(U=QE=C(V-E)E\)
コンデンサーに蓄えられるエネルギーは
\(U=\displaystyle\frac{1}{2}CV^2-\frac{1}{2}CE^2\)
よって、エネルギー保存則より
\(\displaystyle\frac{1}{2}CV^2-\frac{1}{2}CE^2=\frac{1}{2}L(\frac{E}{r})^2+C(V-E)E\)
\(V^2-E^2=\displaystyle\frac{L}{C}(\frac{E}{r})^2+2VE-2E^2\)
\(V^2-2VE-\displaystyle\frac{L}{C}(\frac{E}{r})^2+E^2=0\)
解の公式を活用するしかなさそうです
\(V=E+\sqrt{E^2-(-\displaystyle\frac{L}{C}(\frac{E}{r})^2+E^2)}\)
\(V=E+\sqrt{\displaystyle\frac{L}{C}(\frac{E}{r})^2}\)
\(V=E+\displaystyle\frac{E}{r}\sqrt{\frac{L}{C}}\)
\(V=E+I_0\sqrt{\displaystyle\frac{L}{C}}\)
(リ)略 \(E\)
(ヌ)略 \(-\displaystyle\frac{V}{R}\)
(ル)略 \(E-V\)
(ヲ)略 \(I-\displaystyle\frac{V}{R}\)
問2
\(\Delta I_1 + \Delta I_2=0\)について
(リ)(ル)より
\(\displaystyle\frac{E}{L}\Delta t_1 + \frac{E-V_0}{L}\Delta t_2 =0\)
\(\Delta V_1 + \Delta V_2=0\)について
(ヌ)(ヲ)より
\(-\displaystyle\frac{V_0}{CR}\Delta t_1 + \frac{I_0-\frac{V_0}{R}}{C}\Delta t_2 =0\)
\(\Delta t_1 = \alpha \Delta t_2\)なので
\(\displaystyle\frac{E}{L}\alpha\Delta t_2 + \frac{E-V_0}{L}\Delta t_2 =0\)
\(-\displaystyle\frac{V_0}{CR}\alpha\Delta t_2 + \frac{I_0-\frac{V_0}{R}}{C}\Delta t_2 =0\)
\(\displaystyle\frac{E}{L}\alpha + \frac{E-V_0}{L} =0\)
\(-\displaystyle\frac{V_0}{CR}\alpha + \frac{I_0-\frac{V_0}{R}}{C} =0\)
\(\alpha E+ (E-V_0) =0\)
\(-\alpha V_0 + (RI_0-V_0) =0\)
\(E-V_0=-\alpha E\)
∴
\(V_0=E+\alpha t = (1+\alpha)E\)
もう一方の式に代入して整理すると、
\(I_0=(1+\alpha)^2\displaystyle\frac{E}{R}\)
問3
\(V_0=E(1+\alpha)\) であるから、
\(P=\displaystyle\frac{V_0^2}{R}\)
\(=\displaystyle\frac{V^2}{R}\)
\(=\displaystyle\frac{(1+\alpha)^2E^2}{R}\)
一方、図5の抵抗で消費される電力\(P_0\)は、
\(P_0=\displaystyle\frac{E^2}{R}\)
であるから、
\((1+\alpha)^2\)倍
省略した4題については、図を作ってから一緒にアップします。
しばし放置。
