等速直線運動
一直線上を一定の速さで進む運動を等速直線運動と言います。これは小学校で学んだ「速さ×時間=距離」という関係が使えます。
高校になって、何が新しく学ぶところなのかというと、この関係式を全部文字で書きなおすところです。それ以外は全く一緒ですので、文字になっている部分だけが不慣れなだけであって、計算や考え方は中学どころか小学校までの知識で十分対応ができます。
距離は、実際には、元の位置から変化した位置の量を表すので、変位と呼ばれることもあり、\(x\)を使います。
速さは\(v\)、時間は\(t\)を使って、\(x=vt\)と書き表せます。公式の一つではありますが、頑張って覚えましょうというよりも、今までの知識を高校内容に合うように読み替えましょう、という気持ちの方が大切ですね。
▼ 等速直線運動
\(x = vt\)
\(x[m]\):変位(距離)
\(v[m/s]\):速度
\(t[s]\):移動に要した時間
等速直線運動のグラフ

(1)物体が原点から正の向きに移動する場合
図のように小球が移動したとします。図に書き忘れましたが、数字は位置\([m]\)を表していることにします。
このように、時間とともに小球が\(x\)軸正の向きに移動していくとき、速さのグラフと位置のグラフを描いてみることにします。
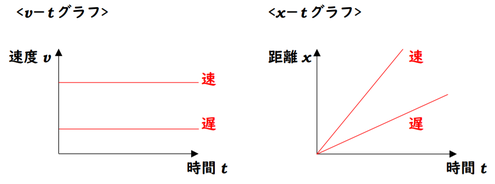
まず速さのグラフを考えます。縦軸を速度\(v\)、横軸を時間\(t\)としたグラフのことを、\(v-t\)グラフと言います。
等速直線運動では、速度が等速ですので、変わらずに一定となります。縦軸の値が大きければ速い運動、縦軸の値が小さければ遅い運動を表します。
次に、位置のグラフを考えましょう。縦軸を変位\(x\)、横軸を時間\(t\)としたグラフを\(x-t\)グラフと言います。
等速直線運動では、1秒間に進む距離は同じですので、ちょうど比例のグラフになります。このとき、グラフの傾きが速さを表すことになり、傾きが急なグラフは速い運動を、傾きがゆるやかなグラフは遅い運動を表します。

(2)物体が、ある位置\(x_0\)から移動する場合
中学では、主に原点からの運動しか扱いませんでした。ところが高校ではより一般的に、図のように、原点ではない位置から運動が始まる場合も扱います。しかも移動する向きも、左右どちらにすすむ場合を扱います。
この場合、グラフの概形はどうなるでしょうか。

まず\(v-t\)グラフについて、グラフは横一直線なのは変わりませんが、左に進む場合、\(x\)軸の負の向きに進みますので、こういう場合、速度が負となります。
グラフの値もマイナスをとることもあるわけですね。
次に\(x-t\)グラフ。こちらも左向きに進むと、位置が\(1.0m\)、\(0m\)、\(-1.0m\)、と変化していきますので、傾きは負となり、やがてグラフはマイナスの領域に伸びていきます。
このとき、グラフの交点が、小球が原点を通る時間を意味します。
