合成速度

大阪の梅田にエスカレーターを平地に置いたような、動く歩道っていうものがあるんですね。写真は羽田空港のものですが。
大きな荷物を持っている旅行者からすると、この上を歩けば高速に安全に移動できるので、ずいぶんと便利です。職員室から私の車をとめている駐車場まで設置しておいてほしいですね。
さて、本題ですが、この上を歩けば、歩道の外にいる人から見たときに速度が速くなっているように見えます。
逆走する人は聡明な大人にはいないでしょうが、仮に逆走すれば、本来の歩くスピードより遅く見えるのもイメージできますね。
なぜそんな風に見えるのか、それは単純な話で、動く歩道の速さと、歩行者が歩く速さが合計されているからです。このように速度は足し算引き算が可能で、このときに合計した速度のことを合成速度といいます。
直線上の速度の合成
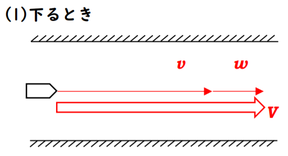
静水(流れのない水面)に対して速度\(v\)で進む船があったとします。この船が、速さ\(w\)で流れる川を下ることを考えてみましょう。
すると、本来であれば速度\(v\)で進むはずですが、川に流されて、さらに\(w\)だけ速度アップします。
結果として、合成速度は \(V=v+w\) で表されます。
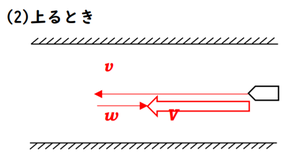
逆に、川の流れにさからって、上流へ頑張って進むことを考えてみましょう。
今度は、せっかく速さ\(v\)で進んでも、川の流れのために逆向きに\(w\)の速さ分だけ流されてしまいますので、合成速度は \(V=v-w\) となります。
このように、直線上の合成速度は単純に足し算と引き算で説明することができます。公式としてしまってもいいですが、公式というほどのものでもないですので、暗記に走らないように気を付けましょう。
平面上の速度の合成
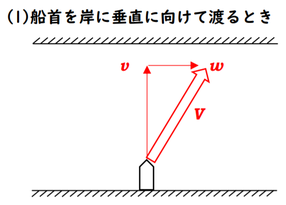
同じように、平面上の合成速度について考えてみましょう。今度は、川の流れる向きと、船が進む向きが違う場合を考えます。
このときも、考え方は同じですが、計算式は少し複雑になります。
船の先を岸に垂直に向けて進んだとします。すると速さ\(v\)で進んでいきますが、川の流れによって川下に向かって\(w\)で流され、図の太矢印の向きに船が進みます。
こうなってくると、合成速度は単純に足し算で表すことはできず、三平方の定理を使うことになります。
三平方の定理より、合成速度は
\(V=\displaystyle\sqrt{v^2+w^2}\)
となります。
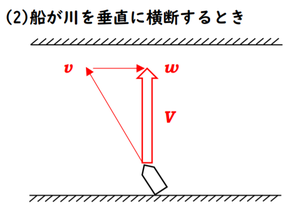
では、岸に対して垂直に進みたいときはどうすればいいでしょうか。
この場合は、あらかじめ少しだけ船の頭を川上の方に向けておいて、船を進ませてやるといいですね。どのくらい川上に向けておけばいいかというと、船が速さ\(v\)で進んだあと、川によって\(w\)だけ流された結果、太矢印が川に対して垂直となるように上手に角度を調節することになります。
同じく三平方の定理より、合成速度は
\(v^2=V^2+w^2\)
と書けるので、移項して
\(V^2=v^2-w^2\)
よって
\(V=\displaystyle\sqrt{v^2-w^2}\)
となります。
