(1)
船の速さは\(4.0m/s\)、川の流速は\(2.0m/s\)なので、岸から見た船の速さは、川を上るときは流速分遅くなって\(2.0m/s\)、川を下るときは流速分速くなって\(6.0m/s\)ですね。
よって、要する時間は「距離÷速さ」より
上り:\(t_1=72÷2.0=36s\)
下り:\(t_2=72÷6.0=12s\)
となります。
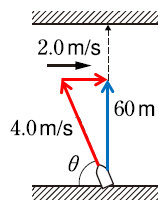
(2)
川に流れがあるので、川を直角に渡ろうとするなら、少しだけ船の頭を川上の方向に向けなければいけません。
では、どのくらい傾ければいいのかということですが、図のように、少し上流側に傾けて\(4.0m/s\)で進んだあと、川に\(2.0m/s\)分だけ流された結果、実際に進んだのは青矢印のように岸に垂直になったと考えます。
これがちょうど\(1:2:\sqrt{3}\)の関係になっているので、\(θ=60°\)と求まります。
\(θ\)は「シータ(theta)」と読み、高校物理と高校数学では角度を表す文字としてよく使われます。
(大学では温度を表すときもあります)
(3)
(2)より、\(1:2:\sqrt{3}\)の関係が分かっているので、青矢印の部分の速さは\(2\sqrt{3}m/s\)であることがわかります。
この速さで川幅\(60m\)を渡るので、「距離÷速さ」から
\(t=\displaystyle\frac{60}{2\sqrt{3}}\)
有理化して(分子分母に\(\sqrt{3}\)かけて)
\(t=\displaystyle\frac{60\sqrt{3}}{6}\)
\(t=10\sqrt{3}\)
\(t≒10×1.73\)
\(t=17.3\)
\(t≒17s\)
\(\sqrt{3}≒1.73\)は暗記です。\(\sqrt{2}\)から\(\sqrt{7}\)くらいまでは覚えておきましょう。
また、問題文がすべて2ケタで与えられているので、解答も2ケタになるように四捨五入します。
\(17.3s\)は途中式扱いで減点されると思っておくといいでしょう。
