(1)
相対速度でややこしい日本語の問題ですが、「に対する」を「から見た」に読み替えることですっきりします。
「\(A\)に対する\(B\)の相対速度」を「\(A\)から見た\(B\)の速度」と読み替えましょう。
図の東向きを正とすると、\(A\)の速度は\(+10m/s\)、\(B\)の速度は\(-15m/s\)であることに注意して、
相対速度\(=\)相手の速度\(-\)自分の速度 より
相対速度\(=(-15)-10\)
相対速度\(=-25m/s\)
東向きに\(-25m/s\)ということなので、最終的な解答は
西向きに\(25m/s\)となります。
東向きに\(-25m/s\)は途中式とみなされて不正解です。
(2)
平面での相対速度は「相手-自分」の公式が使えません。
平面での相対速度は
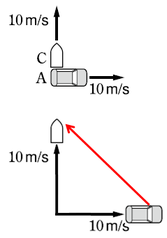
step1:同じところから移動していることにする
step2:「自分」から「相手」へ目線を引く
step3:目線の長さと向きが相対速度を表す
の手順に従って解いていきます。
手順をなぞっていくと図のようになりますので、\(1:1:\sqrt{2}\)の関係が見えてきます。
よって、
相対速度\(=10\sqrt{2}\)
相対速度\(≒10×1.41\)
相対速度\(=14.1\)
相対速度\(≒14m/s\)
となります。解答は問題文に合わせて2ケタに揃えます。
最終的な解答は
北西の向きに\(14m/s\)
「速さ」を求める問題の場合、大きさだけ求めればいいですが、「速度」を求める場合は向きと大きさの2問を聞いている意味の日本語ですので、向きがない場合は点数は半分しかもらえません。
速さ:大きさのみ
速度:向きと大きさ
という関係を知っておきましょう。
