等加速度直線運動
中学理科では、等速直線運動については計算問題も扱われていましたが、加速したり減速したりする運動に関しては現象だけで終わらせていて、計算問題までは触れられずにいました。高校では、この分野にも切り込んでいきます。
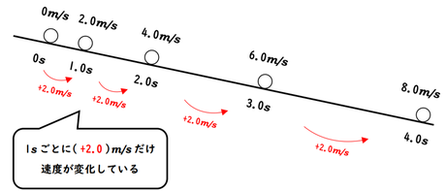
斜面上に小球を静かにおいて、手を離したとします。するとだんだん加速していき、図のように\(1.0s\)後に\(2.0m/s\)、\(2.0s\)後に\(4.0m/s\)という速さの変化があったとします。
このときに、速さがだんだんと速くなるのは直感的にも理解できますが、具体的にどのくらい速くなっていっているのかを決めようと思います。図を見てください。速さがどのくらい増えているかを赤文字で示しました。
速さはランダムな値で増えているわけではなく、\(1.0s\)ごとに\(+2.0m/s\)になる、しかもその量は途中で変わることなく、ずっと\(+2.0m/s\)のままである。こういうとき、\(+2.0m/s\)のように\(1s\)ごとに速くなる割合のことを加速度といい、この加速度がずっと等しい運動のことを等加速度運動といいます。
ここではさらに、運動が直線状であるので特段、等加速度直線運動と呼びます。
等加速度運動には、等加速度円運動というものもあって、物理基礎ではなく専門の物理の単元で学びます。なので、等加速度運動のうち、直線運動に絞って考えていますよ、ということで、等加速度直線運動の方を重要用語として知っておきましょう。
これについては、次の章で深追いします。
(復習 物基4 等速直線運動)
加速度
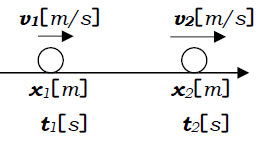
上で簡単に話した加速度をきちんと立式しておこうと思います。
加速度は\(1s\)間に、どのくらいの速度の変化があったかを表す量です。なので、まず速さの変化分\(Δv=v_2-v_1\)を求めておいて、それを時間\(Δt=t_2-t_1\)でわり算してやると、定義することができます。加速度をアクセルの頭文字\(a\)で表してやって、
▼加速度
\(a=\displaystyle\frac{Δv}{Δt}\)
\(a[m/s^2]\):加速度
\(Δv[m/s]\):速度の変化
\(Δt[s]\):時間
と公式化することができます。
加速度の単位\([m/s^2]\)は「メートル毎秒毎秒」と読みます。
物理をやってる人からすると当たり前な呼び方ですが、慣れるまでは不思議な感じがしますね。
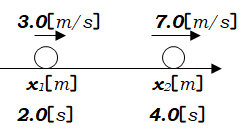
仮に、時刻\(2.0s\)のときに\(3.0m/s\)で運動していた小球が、時刻\(4.0s\)のときには\(7.0m/s\)で運動しているとすると、加速度はいくらになるのか考えてみます。
速度の変化\(Δv\)は、\(7.0-3.0=4.0m/s\)だけ速くなっています。
これが時間\(Δt=4.0-2.0=2.0s\)間で起きているので、
\(a=\displaystyle\frac{Δv}{Δt}=\frac{4.0}{2.0}=2.0m/s^2\)
と求めます。これが加速度の計算です。
瞬間の加速度
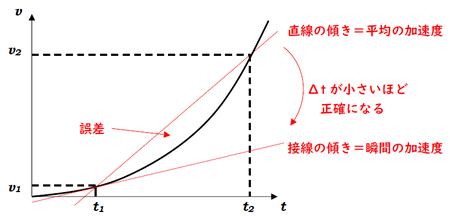
加速度の考え方も、速度のときと同じように「平均の加速度」と「瞬間の加速度」とがあります。
宇宙のかなたから地球に落ちてくる隕石のように、最初はほぼ無重力で加速度もほぼ0だったけど、地球に近づくにつれて徐々に地球の重力加速度の大きさまで大きくなっていく、なんていう現象が考えられます。
加速度も、速度と同じように、常に一定であるとは限りません。なので、瞬間の加速度を出すために、考える時間間隔を極力小さくして、瞬間の加速度という概念を作っておきます。
▼瞬間の加速度
\(a=\displaystyle\frac{dv}{dt}\)
ここでも、「平均」なら「\(Δ\)」で表しますが、「瞬間」なら、そのままアルファベットの「\(d\)」を使って、差を表しています。
(復習 物基5 平均の速度と瞬間の速度)
