
(1)
斜面を水平方向に加速させたところ、斜面に摩擦がないにも関わらず、小物体は滑り落ちなかったという設定です。
これは、物体と同じく移動する座標系から見たとき、斜面が加速する向きと逆向きに押し付けられるためですね。
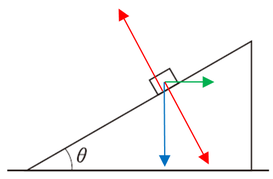
このとき、斜面の加速度と逆向きの「見かけの加速度」を「慣性加速度」といい、これによって発生するような力、この問題では斜面に押し付けられる力のことを「慣性力」と言います。
この「慣性力」と、もともと小物体にかかっている「重力」との合力が、ちょうど垂直抗力の方向とそろえば、小物体は斜面の上にも下にも進まないことになります。
で、その大きさは、\(tan\)を使うのが一番早く求められそうです。
\(tanθ=\displaystyle\frac{慣性力}{重力}\)
\(tanθ=\displaystyle\frac{ma}{mg}\)
よって
\(a=gtanθ\)

(1)別解
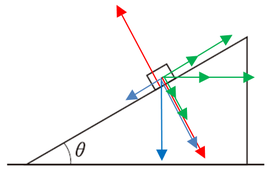
慣性力と重力を、それぞれ斜面方向と斜面に垂直な方向に分解します。図の中には大きさを書くのを省略していますが、上手に\(θ\)を取ってやると、斜面方向の力は、
慣性力:斜面上向きに\(macosθ\)
重力:斜面下向きに\(mgsinθ\)
となり、これがつり合うとき、小物体が斜面上にも斜面下にも進まないので、
\(macosθ=mgsinθ\)
\(a=\displaystyle\frac{gsinθ}{cosθ}\)
\(a=gtanθ\)
(2)
斜面の加速度が2倍になると、慣性力も2倍の\(2a\)になります。
すると、分解した後の、斜面方向上向きの力も2倍の\(2macosθ\)になるので、力のつりあいは解除されて、小物体は斜面上向きに進みます。
こうなると解法は、力のつりあいではなく運動方程式に変わります。
斜面上向きを正として、小物体の斜面から見た加速度を\(α\)とすると、
\(mα=2macosθ-mgsinθ\)
\(α=2acosθ-gsinθ\)
(1)より \(a=gtanθ\) なので、
\(α=2・gtanθ・cosθ-gsinθ\)
\(α=2gsinθ-gsinθ\)
\(α=gsinθ\)
