リ物　基57

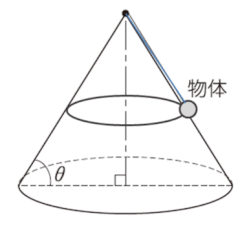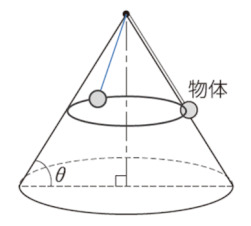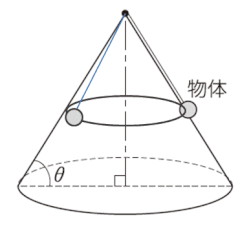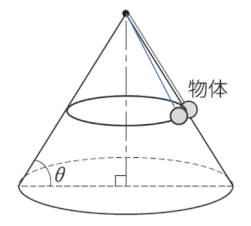
　(1)では、物体が円錐の表面に沿って回転しているときの問題で、物体が円錐から受ける垂直抗力を考慮して解きます。

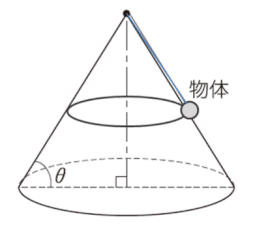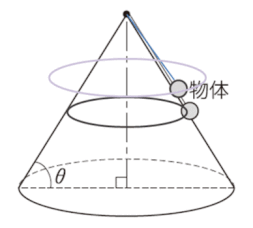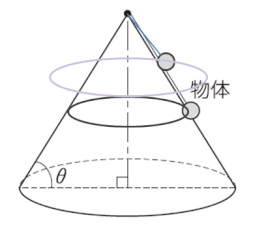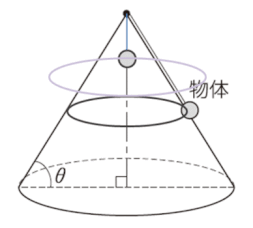
　(2)では、回転速度(角速度)を大きくしていくと、やがて物体は円錐の表面に沿うことなく、円錐表面から浮いて円運動を始めます。垂直抗力がなくなります。

　ここでの図は、誇張して、完全に円錐から離れて円運動をしているgifアニメにしていますが、問われているのは、ちょうど垂直抗力が0になるときなので、見た目の運動状況はほぼ円錐表面に沿って物体が動くことになります。

　そうすることで\(θ\)がそのまま使えるのでいいですね。

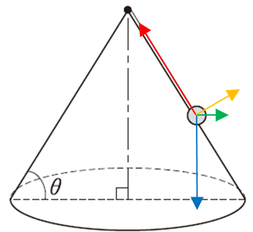
(1)

物体とともに動く座標から見たとき、物体にかかる力は４つ。

張力、垂直抗力、遠心力、重力があります。

それぞれの大きさは、

張力\(=S\)

垂直抗力\(=N\)

遠心力\(=F=mrω^2\)

重力\(=mg\)

ですね。

これらをきちんと処理するためには、適切な軸を選ぶ必要があります。

ひとつは、そのまま縦横の軸をとる方法、もう一つは、斜面方向と斜面に垂直な方向を軸に取る方法があります。

軸のとり方は慣れれば最短をすぐに見つけることができますが、最初のうちはどちらかでやってみて、うまくいかなければもう一つの軸のとり方で解いてみると良いと思います。

ここでは、斜面方向と、斜面垂直方向の軸を考えることにします。

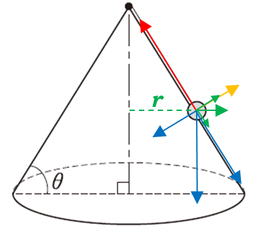
遠心力について、あらかじめ準備をしておきます。

遠心力の公式は\(mrω^2\)ですが、\(r\)は円運動の半径であって、問題文には与えられていません。なので、糸の長さ\(l\)を用いて、\(r=lcosθ\)としておきます。

すると、遠心力の大きさは、

\(F=mrω^2=mlω^2cosθ\)　　…(答)

となります。

これを、斜面軸と斜面垂直軸に分解して、それぞれ力のつりあいを取ると、

斜面軸：\(S\)\(=\)\(mlω^2cos^2θ\)\(+mgsinθ\)　　…(答)

斜面垂直軸：\(N\)\(+mlω^2sinθcosθ\)\(=\)\(mgcosθ\)

これを移項して\(N\)も求まりますね。