
非等速円運動の問題なので、エネルギー保存則と力のつり合いを使うのが指針です。
(1)
最高点を通過するときの速さを求める場合、物理基礎の内容であれば、力学的エネルギー保存則を使いました。
ところが、この問題では、最下点での速さ\(v_0\)が与えられていないので、力学的エネルギー保存則では解けません。
そこで別の作戦を立てる必要がありますが、非等速円運動の問題を解くときの観点として、エネルギー保存か、力のつり合いのどちらかを考えますので、保存則が使えないとなれば、次に思いつくのが力のつり合いです。
最高点で、重力より遠心力が強ければ、小球は落ちることなく回転を続けることができます。遠心力が強いということは、垂直抗力もはたらきます。
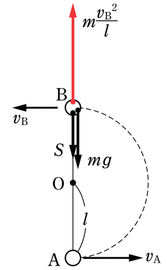
垂直抗力を\(S\)、小球にはたらく遠心力を\(m\frac{v_B^2}{l}\)、重力を\(mg\)とすると、
最高点での力のつり合いの式は、
\(S+mg=m\displaystyle\frac{v_B^2}{l}\)
小球が最高点をギリギリ通過するかしないかの境界では、一瞬だけ垂直抗力が\(0\)になります。
なので、
\(mg=m\displaystyle\frac{v_B^2}{l}\)
よって、\(v_B\)について解くと、
\(v_B=\sqrt{gl}\)
計算過程は省略しました。
(2)
最高点での速さが分かれば、最下点での速さは、今度は力学的エネルギー保存則で求めることができます。
\(\displaystyle\frac{1}{2}mv_0^2=\frac{1}{2}mv_B^2+mg・2l\) から
\(mv_0^2=mv_B^2+4mgl\)
\(v_0^2=v_B^2+4gl\)
(1)で \(v_B=\sqrt{gl}\) が分かってますので、代入して
\(v_0^2=gl+4gl\)
\(v_0=\sqrt{5gl}\)
(3)
糸ではなく、重さのない棒を用いた場合、(1)の結果が変わります。最高点で、遠心力に頼って壁に張り付く必要がなくなりますので、速さが\(0\)以上でさえいれば通過できてしまいます。
最下点での力学的エネルギー=最高点での力学的エネルギー
だと、最高点に到着したときに、ちょうど小球の速さが\(0\)となり実験終了となってしまいますので、ここからわずかにでも大きいエネルギーがあればいいことになります。等号成立しませんので、それを注意しましょう。
よって、
最下点での力学的エネルギー>最高点でのエネルギー
\(\displaystyle\frac{1}{2}mv_0^2>mg・2l\)
\(v_0^2=4gl\)
\(v_0=2\sqrt{gl}\)
