慣性の法則(復習)
運動の第一法則(慣性の法則)
物体系の外部から力を受けないか,受けていても合力が0の場合,静止している物体は静止し続け,運動している物体は等速直線運動を続ける。
物体は,それまでの運動を続けようとする性質(慣性)を持ちます。この法則を丸々覚えようとすると大変なので,つまりどういうこと?という部分を強調するなら,「力を加えていないなら,速度は常に一定」ということを意味している法則です。
速度が0であるなら,速度は0のまま。速度が何かしら値を持つなら,それと同じ値でずっと動き続けるわけなので等速運動,しかも力が加わらないなら物体は曲がることもないので,さらに直線運動でもあるわけですね。まとめて等速直線運動というわけです。
この慣性はどこから発生しているのかというと、「質量」が原因になっているようです。質量が大きいほど慣性は強く働き、質量が0の物体には慣性はありません。
慣性力
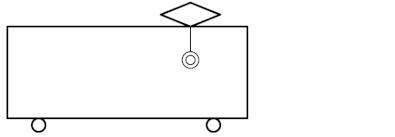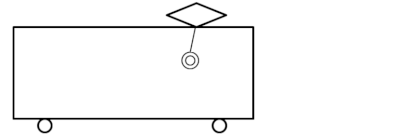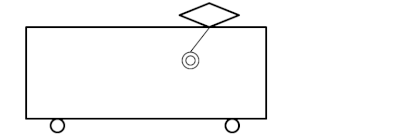
ある電車が加速度\(a\)で急発進したとします。
すると、電車の中のつり革の部分には慣性の法則が働くので、電車の外から見たとすれば、つり革の部分だけが電車の進行から置いていかれているように見えるはずです。
つり革のひも、伸びてますね…。そのうち直すかもしれません。
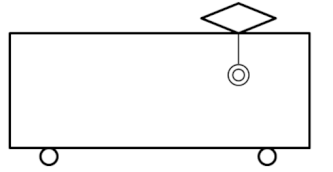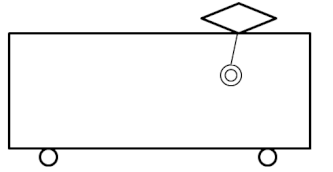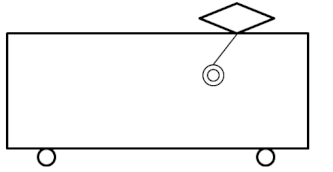
一方で、電車の中から同じ光景を見たとすると、つり革の方が、電車の進行方向と逆向きに加速度\(a\)で引っ張られているように見えるはずですね。
まるで「見かけの重力」が進行方向の後ろ向きに働いているように錯覚します。
このように、見ている場所によっては「見かけの力」が発生しますが、この力のことを「慣性力」と呼びます。
そして、効果は質量に比例しますので、大きさは\(ma\)です。
▼慣性力
\(F=ma\)
向きは実際の加速度と逆向き
慣性系と非慣性系
電車の外からつり革を見るとき、慣性の法則が成立していることがわかりました。このように、慣性の法則が成立するような座標系のことを「慣性系」と呼びます。
細かい話をすると、慣性系には、電車の外の世界のように静止している座標系と、等速運動をしている座標系があります。電車のつり革も、斜めになるのは発車したての加速中と、停止直前の減速中だけで、等速運動している区間では斜めになりませんので、静止しているのと同じです。
一方で、加速中の電車の中の世界のように、「見かけの力」がはたらくような座標系は「非慣性系」といい、「加速度系」や「回転系」があります。
言い換えると、「加速度系」や「回転系」が出題されたときには「慣性力」が関わる問題だということに気付く必要が出てきます。
慣性力の向き
とてもシンプルです。
慣性力の向きは実際の加速度の向きと逆向き。
以上。それだけです。
簡単に練習しておきましょう。
問:鉛直上方に\(a=1.0m/s^2\)で上昇しているエレベーターの中に、質量\(50kg\)の人がいる。(\(g=9.8m/s^2\)とする)
(1)人にはたらく慣性力の向きと大きさはいくらか。
(2)人が感じる見かけの重力の大きさはいくらか。
解:
(1)向きは実際の加速度と逆向きなので、「鉛直下向き」ですね。
大きさは \(ma=50×1.0=50N\) です。
(2)実際の重力の大きさは \(mg=50×9.8=490N\)ですが、ここに鉛直下向きの「見かけの重力」が追加で\(50N\)加わります。
よって、 \(490+50=540=5.4×10^2N\) です。
公式ではありませんが、
▼見かけの重力の合成
人が感じる重力=実際の重力±見かけの重力
ということですね。見かけの重力はエレベーターが上に進むか下に進むかで変わるので注意してください。
