非慣性系における見かけの力
慣性の法則が成立しない座標系を非慣性系と呼んでいました。簡単に言うと、見かけの力がはたらく座標系のことです。
具体的には「加速度系」と「回転系」がありますが、それぞれの見かけの力には名称がついていますので、確認しておきましょう。
慣性力:加速度系における見かけの力
\(F=ma\)
遠心力:回転系に対して静止している物体にはたらく見かけの力
\(F=mr\omega ^2 = m \displaystyle\frac{v^2}{r}\)
コリオリ力:回転系に対して運動している物体にはたらく見かけの力
\(F=2mv\omega\)
このうち、コリオリの力に関しては、高校ではほとんど扱われませんので、覚えなくても構いません。
しかし、大阪工業大学など一部の大学の入試問題で出題されることはあります。それでも、そのときは誘導に乗っかって解く形になるので、やっぱり覚えてなくても構いません。
遠心力
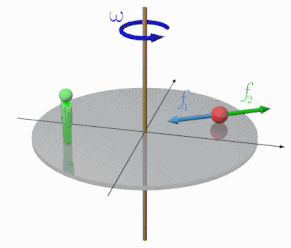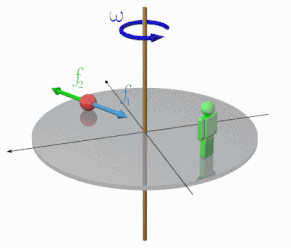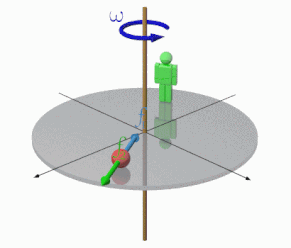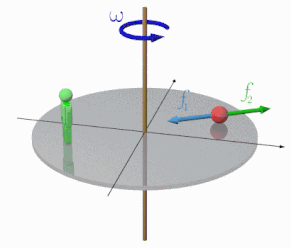
等速円運動をしている物体を、円運動の外の観測者から見ると、中心へ向かう向きへ「向心加速度」を受けながら回転しているように見えます。
このときの運動の振る舞いを式で表そうと思えば、等速円運動をしているので、円運動方程式を使えばよかったですね。
こんどは、円運動している物体と同じ速さで観測者も回転しているとして、この観測者から見た物体の運動の振る舞いを考えてみようと思います。
画像のように、円運動する観測者から見ると、物体は静止しているように見えるはずです。円運動をしているから向心力がはたらいていますが、本当に向心力のみがはたらいているだけだったら、ものの数秒で物体は中心に"落ちる"はずです。
そうならないのは、運動座標から見たときには「見かけの力」がはたらくためです。運動座標が直線状のときには、この力のことを「慣性力」と呼んでいましたが、円状のときには「遠心力」と呼び替えることにします。
慣性力は、本来の加速度と逆向きで同じ大きさなので、円運動の場合は、円の中心から外向きに、\(mr\omega ^2\)、もしくは\(m\displaystyle \frac{v^2}{r}\)と式で表すことができます。
図の円運動で、仮に物体が軸に糸でつながれているのであれば、張力を\(T\)として、\(f_1=T\)と書けます。
一方で遠心力は\(mr\omega^2\)なので、
\(T=mr\omega^2\)
という式を立てることができますね。あとはその問題が何の文字について問うているのかによって、その文字に向かって式変形していけばいいことになります。
基本的な考え方はこんな感じです。あとは問題パターンによって細かい知識が必要になってくるでしょうから、それは問題演習をしていく中で都度おさえていきましょう。
