一直線上の力の合成

ある物体を右に\(2.0N\)の力と\(3.0N\)の力で引っ張ります。このとき、合わせて\(5.0N\)で引っ張ることになるので、はじめから\(5.0N\)の力1つだけが物体にかかっていると考えることもできます。
このように、複数の力を合わせて1つの力にすることを「力の合成」といい、その力を「合力」といいます。
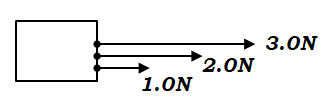
3力を合成するときも、そのまま足してやればいいですね。この図の場合であれば、\(1.0+2.0+3.0=6.0N\)です。

右向きを正としたとき、左向きは負になるので、この図のように、合力がちょうど0になる場合もあります。
式で書けば、
\(2.0+1.0-3.0=0N\)
ですね。
もし、左向きの\(3.0N\)が、\(4.0N\)になれば、合力はマイナスになりますが、右向きを正としてマイナスの値が出たということは、左向きの力がかかっているんだな、と解釈することができますので、符号が向きを表すことになります。
▼一直線上の力の合力
\(F=F_1+F_2+F_3+…\)
\(F=\Sigma F_i\)
平面上の力の合成

合成したい2力が一直線上にない場合は、どのように求めればいいでしょうか。
中学理科で学習済だとは思いますが、確認しておきましょう。
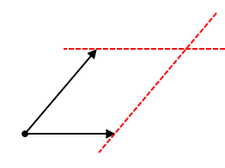
2つの力が、平行四辺形の辺になるように作図するといいんでしたね。
1つの矢印の平行線を、もう1つの矢印の先に合わせて引きます。

すると、元の矢印と補助線とで平行四辺形ができますので、その対角線に向かって線を引いてやると、合力を作図することができますね。
▼平面の力の合成
平行四辺形の対角線を作図する
有名角の合力

高校ではあまり使うことはありませんが、中3理科で登場してくる有名角の合力を一応復習しておきます。
同じ\(10N\)の大きさの2力が合成されるとき、その2力の角度が、ある値を取るときに限り、計算が三平方の定理によって導出できます。
導出は省きますが、結果として、
2力のなす角が、
\(120°\)のとき、合力は\(10N\)
\(90°\)のとき、合力は\(10\sqrt{2}[N]\)
\(60°\)のとき、合力は\(10\sqrt{3}[N]\)
になります。必須暗記ではありませんが、知っていてもいいでしょう。
力の分解

今度は逆に、1つの力を2方向に分けてやる場合のことを考えます。
このとき、力を分けることを「力の分解」といい、分けた力のことを「分力」と言います。
まず、力を分解したい方向に補助線を引きます。力を分解したい方向がどちらか、ということは、それ自体が問題にできそうな話ですが、それについては、もう少し先の話で触れることにしましょう。
ここでは先に2方向を示しておきます。

片方の補助線に注目して、その補助線と平行な線を、力の矢印の先に合わせて引きます。
このとき、正式には三角定規を2つ使うなどして作図してやるんでしょうが、一つの作図にわざわざそんな作業をしていたのでは、高校物理では先に進むのにものすごい時間がかかってしまいますので、フィーリングでいいです。
こんな感じで平行っぽいかな、くらいでいいです。よほど下手じゃない限り、肉眼では平行にみえるでしょう。きっと。

もう片方の補助線でも同じ作業をしてやります。
平行線は、矢印の先に合わせて引いてください。たまに間違えて、補助線の先に合わせて引いてしまう人がいますが、補助線の終わりは特に意味を持たない端点なので、合わせてはいけません。

補助線同士が重なる交点を2か所探してやります。

その2か所に向かって分力が作図されます。
これで終了。
