接触力と遠隔力
物体が受ける力は、必ず他の物体から受けます。相手が何もないのに、力だけが勝手に加えられるということはあり得ません。
一般的には、触れないと力は加えることができません。このとき、触れることで及ぼす力を総称して「接触力」といいます。
接触力にはいろんなものがありますが、よく出てくるものを紹介します。
▼接触力の例
張力(Tension) \(T\)
垂直抗力(Normal Reaction) \(N\)
摩擦力(Friction) \(f\)
弾性力 \(kx\)
といったものがあげられます。細かい話をすると、垂直抗力と抗力は違うものだ、とか、摩擦力には静止摩擦力と動摩擦力がある、とか、いろいろ挙げられますが、出てくるたびに確認すれば十分ですので、ここでは流しておきます。
一方で、触れていないのにはたらく力も世の中には存在します。それは魔力とか学力とかそういうものではなくて、きちんと物理的に説明できる力です。触れていないのにはたらく力を総称して「遠隔力」といいます。
遠隔力は、現代の科学では、光の速さで伝わるとされていますので、日常生活においては接触力と同じく一瞬で伝播(でんぱ)しますが、冷静に考えると、太陽の光が地球に伝わるのに約\(500s\)かかりますので、今この瞬間に太陽が消滅したとしても、\(500s\)の間だけは太陽の重力をつかって地球は公転を続けることができます。不思議ですね。
遠隔力には次のようなものがあります。
▼遠隔力の例
重力 \(mg\)
静電気力 \(qE\)
磁力
核力
静電気や磁石は、引き合う力やしりぞけ合う力があるにも関わらず、重力は引き合う力しか存在していないことが、長年物理学の間では謎のままです。数式上、反発する重力もある、と提唱する科学者や、真空が反発する重力に相当するんじゃないか、と提唱する科学者もいますが、未知のままです。
理論上の話と実験上の話の両方の整合性が取れて初めて証明となりますが、そのどちらも未完成です。
誰かこの未知の学問にチャレンジしてみませんか?
力のつり合い
物体にはたらいているいくつかの力が互いに打ち消し合う状態、言い換えると、合力が00の状態を、「力がつり合っている」と言います。
力がつり合っているとき、物体は静止していると習った、もしくは認識している人は多いと思いますが、必ずしも静止しているとは限りません。
正確には、力がつり合っているとき、物体は加速したり、向きを変えたりしない。という物理法則ですね。
これは、慣性の法則として知られています。のちのち登場します。
▼つり合いの条件(2力のとき)
2力が、
①同じ大きさ
②互いに逆向き
③同一直線上にある
とき、2力はつり合っている、という。
※静止しているとは限らない。
力のつり合いの問題で、最初に引っかかるのは、力が作図できないという壁です。ここでは細かく触れませんが、いざ問題を解いてみると、そういわれるゆえんが分かると思います。
次に引っかかるポイントとしては、どの物体に、何の力が、どの向きに働いているか分からない、という点です。
結局、つり合いが分からないんじゃなくて、作図が分からないから、その先の何もかもが解けない、という人が多いですので、つり合いが分からなくてこの単元に戻ってきた人は、残念ながら復習すべきは作図です。
つり合いの単元自体は、分かりませんという人はあまりいません。
力のつり合いを簡単に解く方法

一つ、問題を解いてみましょう。
軽い糸に重さ(重力の大きさ)10Nの小球をつけ、天井からつるした。
小球を水平方向に力Fで引き,糸が天井と\(30°\)の角をなす状態で静止させたとき、次の値を求めなさい。
(1)糸が小球を引く力の大きさ\(T [N]\)
(2)力Fの大きさ\(F [N]\)

まずは、教科書通り、きちんと解答までたどってみることにします。
問題文で問われているように、張力\(T\)を適当な長さで作図します。そして、物体には重力もかかっているはずなので、それも適当な長さで重力\(W\)として作図しておきます。
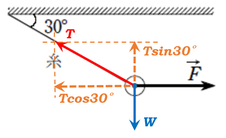
張力\(T\)が斜め向きに作図されていますので、縦軸と横軸の方向へ分解します。
このとき、(図には書いていませんが)錯角の\(30°\)に注目すれば、水平方向の成分は\(Tcos30°\)と取れますので、鉛直方向の力は\(Tsin30°\)と取れますね。
これらが、水平方向には水平方向だけ、鉛直方向には鉛直方向だけで力のつり合いをそれぞれ考えれば、
[水平方向] \(Tcos30°=F\)
[鉛直方向] \(Tsin30°=W\)
となり、今、\(W=10[N]\)であることが問題文に書いてありますので、鉛直方向の式を解いて、
\(\displaystyle\frac{1}{2}T=10\)
よって
\(T=20[N]\)
これを水平方向の式に代入して
\(20×\displaystyle\frac{\sqrt{3}}{2}=F\)
よって
\(F=17[N]\)
として、これで終了です。
しかし、これではちょっとめんどくさいので、私はこの方法では解きません。そもそも張力\(T\)を作図するときに、なんとなくで長さを決めて書くスタートにしているあたり、あいまいさを残してますよね。上手に作図できたからいいものの、もし長さを間違えて書いていたら、ちょっと問題設定が変わったときに、それでも解けるかといわれたら、場合によりますね。
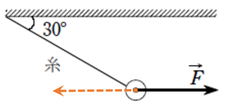
私なら、まず図の通り。
力\(F\)が右にかかっていますが、力はつりあっているはずなので、ちょうど綱引き状態で、反対向きに同じ大きさの力がかかっているはずだ、という作図線を真っ先に残してしまいます。
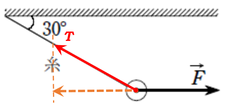
そして、その力は張力\(T\)を分解したうちの一つにならないといけないはずですから、縦線を補助線として引いて、張力\(T\)を作図します。
こうすることで、教科書のように、なんとなく引いた張力\(T\)ではなく、厳密にこの長さになることが分かった上での\(T\)を作図することができます。
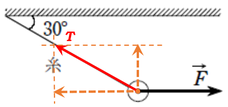
ついでに残りの力も作図しておきます。
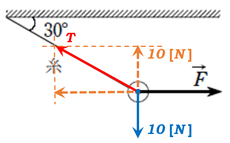
「残りの力」は、重力とつりあうはずなので、つりあうように重力も作図します。
この作図も、教科書の方法と違って、なんとなく引いた下矢印ではなくて、厳密にこの長さ、ということが分かっている状態での”正しい”作図ですね。
重さが\(10N\)と問題文に書いてありますので、上下の矢印とも\(10N\)になります。ここに計算はありません。
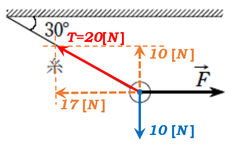
そして、張力を分解した赤線とオレンジ線の作図の方に、辺の比が\(1:2:\sqrt{3}\)の三角形がありますので、張力\(T\)が\(20N\)、張力の水平成分の分力は\(10\sqrt{3}≒17N\)となります。
張力の水平成分の大きさは力\(F\)とつりあっていますので、\(F\)も\(17N\)となります。
このようにたどっていく方が\(sin\theta\)も\(cos\theta\)も使わずに済みますし、変に連立方程式を立てることもありませんので、簡単だと思うのですが、皆さんはどうですか?
