単振動４　単振り子

　軽い糸の先におもりをつけて、おもりを左右に往復させるような運動のことを「単振り子」と言います。

　この運動は、一般的な運動を説明しようと思えば、非等速円運動の話になりますが、往復の幅が極端に小さいときに限れば、ほぼ直線上を運動していると解釈できるので、水平ばね振り子と同じように、単振動の公式が使えるのではないか、という話を扱う分野です。

　だいたい角度にして20°くらいまでなら直線とみなして単振動と考えても、実験値が理論立てて説明できますので、小さい往復幅、というのは、そのくらいの範囲の運動だと思ってください。

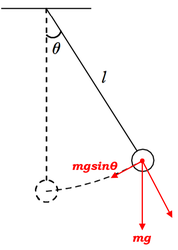
　とりあえず、重力を作図して、分解してみましょうか。

　図のようになりますね。このうち、振り子を中心に戻そうとする分の力が　\(mgsin\theta\)　ですので、これが復元力として働きます。

　往復運動が、ほぼ直線上で行われますので、\(x\)軸を考えて、おもりの最下点を原点とします。いま図のようにおもりが右にずれていますので、位置\(x\)の点に物体があると考えます。

　運動方程式を立てると、右向きを正として、

　　\(ma=-mgsin\theta\)

　　\(-m\omega^2 x=-mgsin\theta\)

　　\(\omega^2 x =gsin\theta\)

となります。ここまでの式変形はあまり悩まずに進められそうです。

ですが、ここで手詰まりですね。これ以上の変形はできませんので、何らかの対策をする必要が出てきます。

　ほぼ直線上なので、図もいっそのこと直線上にしてしまいましょうか。この方が見やすいですね。右向きを正として、左向きの\(mgsin\theta\)にも、マイナスをつけて表記することにしました。

　そして、すぐには納得できないかもしれませんが、\(\theta\)がとても小さいので、図の斜辺の長さと、最下点までの長さは等しいと近似することにします。

　この図だと\(\theta=30°\)くらいありそうなので、見た目では納得しがたいですが、\(\theta=1°\)くらいで作図をすると納得できるでしょう。

　\(\theta\)が十分小さいとき、物理でよく使う近似として、\(sin\theta≒tan\theta\)　というワザがあります。

▼\(\theta <<1\)のときの(一次)近似

　\(sin\theta≒tan\theta≒\theta\)

　これを使うと、

　　\(\omega^2 x ≒ g tan\theta\)

　　\(\omega^2 x = g \displaystyle\frac{x}{l}\)

　　\(\omega^2 = \displaystyle\frac{g}{l}\)

　　\(\omega=\displaystyle\sqrt{\frac{g}{l}}\)

と変形できるので、角振動数を求めることができますね。