単振動

天井にばねをつけて、その下におもりを吊り下げて振動させます。すると、おもりは上下に振動を始めます。このような運動を「単振動」と呼びます。
この図は運動の一例で「鉛直ばね振り子」と言われるものですが、この単元では、このように往復の運動をする物体について学習していきます。
ほかにも、この図を横向きにした「水平ばね振り子」、催眠術師が5円玉を往復させるような「単振り子」、摩擦のある面でばねの先におもりをつけて往復させる「減衰振動」といった内容が、この単元にかかわり深い内容です。
まずはシンプルな用語の確認から。運動の様子が、きれいなサインカーブ(正弦曲線)を描いていますので、物理基礎や中1の音の単元で学習した波の知識の復習をするくらいで大丈夫です。
振動の中心から上端、もしくは下端までの長さのことを振幅\(A[m]\)と言います。また、\(1\)往復にかかる時間を周期\(T[s]\)、\(1s\)間に振動する回数を振動数\(f[Hz]\)と言います。
周期と振動数は、その定義から、
\(1\)往復:\(T[s]\) = \(f\)往復:\(1s\)
と書けますので、
\(fT=1\)
という関係があります。これは物理基礎の波動と同じく、公式というほどのものではありませんが、よく使うので公式化して暗記しておくと便利です。
▼用語確認
振幅\(A[m]\) 振動中心から振動端部までの長さ
周期\(T[s]\) \(1\)往復に要する時間
振動数\(f[Hz]\) \(1s\)間の往復回数
▼周期と振動数の関係
\(fT=1\) \(f=\displaystyle\frac{1}{T}\) \(T=\displaystyle\frac{1}{f}\)
角振動数
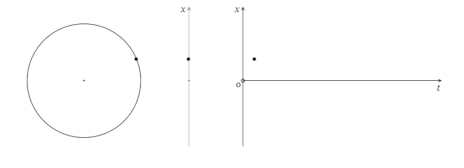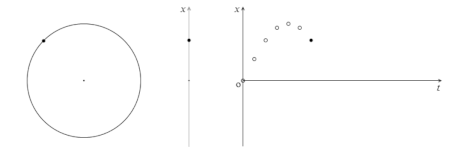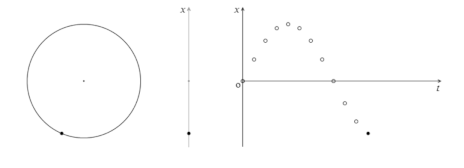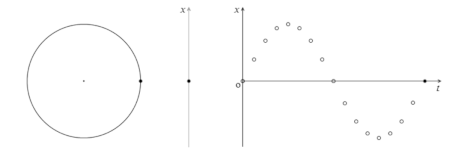
単振動の運動の様子を表すとき、円運動を持ち出すと、考え方がシンプルになります。
円運動をしている物体の横から光を当てて、その影を追いかけたとき、影の運動がちょうど単振動の運動の様子となります。
つまり、わざわざ単振動のための公式を新たに作らなくても、円運動と重複させられるところは重複させてしまった方が、結果的には覚えることも少なくて済むわけです。
円運動と考え方をかぶせるために、新しい概念を一つ設定しておきます。円運動では、\(1s\)間に何度(何ラジアン)回転するか、という量として、角速度\(\omega\)を導入しました。しかし単振動では、運動の様子が似ているとは言え、さすがに円軌道上を運動しているわけではありませんので、用語だけ変えて「角振動数」ということにします。
少し専門的な話になりますが、「等速」円運動の影をうつして考える単振動では、慣例で「角振動数」という用語を使いますが、「非等速」円運動の影をうつして考える振動現象を考えるときは、そのまま「角速度」を使うこともあります。
このあたりの話は高校では扱いませんので、特に気にしなくてもいいです。
▼角振動数と角度の関係
\(\omega=\displaystyle\frac{\theta}{t}\)
\(\theta=\omega t\)
\(1s\)間に何度回転しているかを表す量が\(\omega\)でしたから、\(t[s]\)間での回転角を\(\theta\)と置くことで関係を表しています。
単振動の位置
位置については、きれいなサインカーブを描いていますので、振動中心を原点\(x=0\)として、振幅を\(A\)とすれば、
\(x=Asin\omega t\)
と書けます。ただ、必ずしも物体は原点を中心に振動しているとは限りませんので、振動中心が、より一般的な\(x=x_0\)という位置にあるのであれば、\(\omega t=0\)のときに\(x=x_0\)であればいいので、少し式を変形して、
\(x=x_0+Asin\omega t\)
となります。さらに、振動は必ずしも振動中心から始まるとも限りませんので、角度\(\omega t\)も最初に\(0\)とは限らず、少しずれているかもしれません。角度のズレを\(\phi\)(ファイ)として、それも考慮して式変形すると、
\(x=x_0+Asin(\omega t + \phi)\)
となります。このとき、\((\omega t + \phi)\)が、ひっくるめて角度に相当する部分であって、位置の相(状態)を表すことから「位相」と呼びます。
この先、理解を助けるために、一般的なものから考えるのではなく、一番単純なものを学んでいこうと思いますので、特殊な条件ですが、振動は振動中心から始まり、振動中心は原点と一致していることとして、最初に示した式を使って説明を進めます。
両方の表記をしますが、学習はじめは特殊条件の方の公式だけ覚えていけば十分です。
▼単振動の位置公式(特殊)
\(x=Asin\omega t\)
▼単振動の位置公式(一般)
\(x=x_0+Asin(\omega t + \phi)\)
単振動の速度
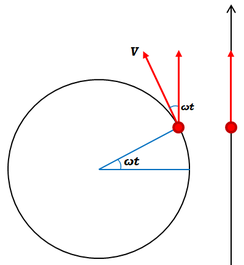
速度も、円運動の影から考えます。円運動上を速さ\(V\)で物体が動いているとき、その縦軸成分は、位相\(\omega t\)を用いて、
\(v=Vcos\omega t\)
と書けます。位相という言葉に不慣れな人は、とりあえず「角度」と同じものだと思っておきましょう。単振動する物体の軌道に角度なんか現れませんから、言葉が違うだけなんだ、というくらいの認識で十分です。正確な知識は、必要になったときにおさえることにします。
ところで、円運動の速さの公式は\(V=r\omega\)でしたので、円軌道の半径を振幅\(A\)で表すのであれば、
\(V=A\omega\)
です。よって、これを代入して、単振動の速度の公式は
\(v=A\omega cos \omega t\)
となります。この式は、振動中心が原点だろうと、ある位置\(x_0\)だろうと同じ形になりますので、一般的な形で表すのであれば、位相の部分だけ修正して
\(v=A\omega cos(\omega t +\phi)\)
となります。
▼単振動の速度公式(特殊)
\(v=A\omega cos \omega t\)
▼単振動の速度公式(一般)
\(v=A\omega cos(\omega t +\phi)\)
単振動の加速度
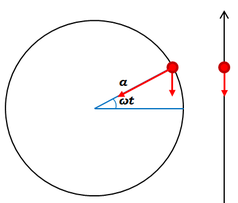
加速度も同じく円運動の影を追っていきます。円運動の加速度は、正式には向心加速度といい、中心の方を向いています。円運動の加速度の大きさを\(\alpha\)、単振動の加速度の大きさを\(a\)として、文字を変えておきます。
この向心加速度の縦軸成分は、
\(a=-\alpha sin\omega t\)
です。また、円運動の加速度の大きさは\(\alpha=r\omega^2\)でしたので、半径を振幅と読み替えて、上式に代入すると、
\(a=-A\omega^2 sin\omega t\)
これも速度と同じく、振動中心の位置によらず決まる量なので、一般の位相であれば
\(a=-A\omega^2 sin(\omega t+\phi)\)
となります。この式の後ろの部分に注目すると、変位が、
[特殊] \(x=Asin\omega t\)
[一般] \(x=x_0+Asin(\omega t + \phi)\)
と書けましたので、\(x\)を使って
[特殊] \(a=-\omega^2 x\)
[一般] \(a=-\omega^2 (x-x_0)\)
と書くこともできます。
▼単振動の加速度公式(特殊)
\(a=-A\omega^2 sin\omega t\)
\(a=-\omega^2 x\)
▼単振動の加速度公式(一般)
\(a=-A\omega^2 sin(\omega t+\phi)\)
\(a=-\omega^2 (x-x_0)\)
くり返しになりますが、入試直前までは、特殊条件(原点スタート、振動中心スタート)の方の公式だけで十分ですので、背伸びして一般条件の公式を使わなくても大丈夫です。
