水平ばね振り子

さあ、ここからは単振動方程式から、いくつかの問題パターンに合わせた運動方程式を作っていきましょう。
壁にばねを取り付け、その先におもりをつけて、水平方向に振動させる単振動のことを「水平ばね振り子」と言います。これは一番シンプルなパターンの問題なので、すぐにマスターできると思います。
指針としては、
① 運動方程式を立てる
② \(\omega\) を求める
③ \(T\)を求める
という流れです。
ばね定数を\(k\)とすると、単振動方程式は、
\(-m \omega^2 x = -Kx\) より
\(-m \omega^2 x = -kx\)
\(\omega^2=\displaystyle\frac{k}{m}\)
よって
\(T=\displaystyle\frac{2\pi}{\omega}\) より
\(T=2\pi \displaystyle\sqrt{\frac{m}{k}}\)
と解いてやります。最終的には解き方まで理解しておいてほしいですが、学習のはじめ頃は、ここで求まった角振動数と周期は、公式として覚えておいてもいいでしょう。
▼水平ばね振り子公式
角振動数
\(\omega =\displaystyle\sqrt{\frac{k}{m}}\)
周期
\(T=2\pi \displaystyle\sqrt{\frac{m}{k}}\)
鉛直ばね振り子

運動が鉛直軸であれば、「鉛直ばね振り子」という運動になります。
鉛直ばね振り子も水平ばね振り子と同じように解けるかと思いきや、実際に問題を解くときに立式してみると、いろんな不都合が生じてしまいます。
一つは重力の扱い。きちんと運動方程式を立てると、式の中に重力が入ってしまって、その処理ができないということが起こります。
もう一つは、ばねの伸びの長さについて。水平ばね振り子と違い、つり合っている時点ですでにいくらかの伸びがありますので、振動中心でばねの伸びが存在しているわけです。この、伸びに関する数式の処理で手詰まりになることもあります。
そして最後に、符号の処理。きちんと向きも考えながら立式したのに、どうしても符号がおかしくなってしまう。でもどこにも間違いは無いように見える。そんなことがよく起こります。
それらの解決策を追いかけながら、公式化していきましょう。
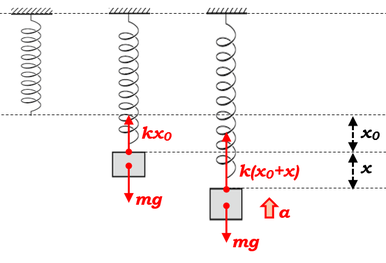
ばね定数\(k\)のばねに、質量\(m\)のおもりを静かにつるして、つり合うようにしたところ、ばねが\(x_0\)だけ伸びておもりが静止したとします。
このとき、つりあいの式は
\(kx_0=mg\)
となります。
ここから\(x\)だけおもりを引っ張ると、弾性力の方が重力より強くなるので、力のつり合いはとれなくなり、運動方程式で表すことになります。
試しに、よくある方法で式を追いかけてみることにします。
鉛直上向きを正として、運動方程式を立ててみると、
\(ma=k(x_0+x)-mg\)
となり、単振動の公式から\(a=-\omega^2 x\)を代入すると
\(-m\omega^2 x=k(x_0+x)-mg\)
となります。単振動の運動方程式は\(\omega\)を求める式なので、\(\omega\)に向かって式変形をしていきたいのですが、右辺が見てのとおり、重たい形になっていて、どうにも式変形は進まなさそうです。
こういう場合、最初に考えていた力のつり合いの式を持ってきて、重力も、ばねの伸びの複雑な部分も一挙に解決させてしまいます。
▼単振動方程式の手詰まり解消法その1
式変形に手詰まったら、つり合いの式を代入する
\(-m\omega^2 x=k(x_0+x)-mg\) より
\(-m\omega^2 x=kx_0+kx-mg\)
ここで \(kx_0=mg\) であるから、
\(-m\omega^2 x=mg+kx-mg\)
\(-m\omega^2 x=kx\)
これで、右辺の重たい式が処理できない、という問題は解決させることができましたね。
ところが、今度は符号の処理に引っかかりました。このまま式変形すると、\(\omega\)は虚数解になりそうです。どこで間違えたでしょうか。どこにも間違えた場所は見当たりません。鉛直下向きを正に取り直して式変形しても、同じ結果に行きつきます。
鉛直下向きを正とすると、
\(m×(-a)=mg-k(x_0+x)\)
\(m\omega^2 x=mg-k(x_0+x)\) より
\(m\omega^2 x=mg-kx_0-kx\)
ここで \(kx_0=mg\) であるから、
\(m\omega^2 x=mg-kx-mg\)
\(m\omega^2 x=-kx\)
やっぱり虚数解になりそうですね。困りました。
▼単振動方程式の手詰まり解消法その2
無意味なマイナスが残るときは、加速度の公式の代入ミスか、変位の符号ミスを検討する
今の式変形の例であれば、加速度の公式の代入ミスはありません。きちんと\(a=-\omega^2 x\)として代入しました。
そもそも、この公式の代入をミスしているときがありますので、その人は、公式をきちんと代入したら問題解決ですね。
では、加速度の公式代入をきちんと行ったにも関わらず符号が合わない人は何について間違えているのでしょうか。
たいがいの場合は、変位の符号のミスが原因となっています。
運動方程式の左辺は、加工することがありませんので、鉛直上向きを正に取ろうとも鉛直下向きを正に取ろうとも\(ma\)で始めます。
右辺については、鉛直下向きを正にとると、鉛直下向きの重力\(mg\)と、鉛直上向きの弾性力\(-k(x_0+x)\)がかかりますので、
\(ma=mg-k(x_0+x)\) より
\(-m\omega^2 x = mg-kx_0-kx\)
つり合いの式\(mg=kx_0\)を代入して
\(-m\omega^2 x=kx_0-kx_0-kx\)
\(m\omega^2=k\)
と式変形が続き、そのまま求めて行けそうです。
鉛直上向きを正にとると、途端に考え方がややこしくなります。鉛直下向きを正にしたときにはあまり気にせずに解いていましたが、いま行っている式変形の原点は、ばねの自然長の点にあります。自然長から下向きを正にして下向きに\(x_0+x\)だけ伸びていることから弾性力の大きさを\(k(x_0+x)\)としてやって、この力の向きが鉛直上向きなので、力全体の符号が逆、ということで\(-k(x_0+x)\)としているわけです。
鉛直上向きを正にとったときの弾性力の大きさは、同じく\(k(x_0+x)\)なんですが、ばねが原点から負の方向に伸びているため、ばねの伸びが\(-(x_0+x\)で書けるため、結局弾性力は\(-k(x_0+x)\)となります。
▼鉛直ばね振り子の復元力の符号
鉛直上向きを正ととっても、鉛直下向きを正ととっても\(F=-Kx\)となる
鉛直上向きを正とすると、
\(ma=-mg-k(x_0+x)\) より
\(-m\omega^2 x = -mg-kx_0-kx\)
このままでは解けませんが、つり合いの式も鉛直上向きを正とすると、ばねの伸びが負ということになるため、\(x_0\)ではなく\(-x_0\)を使いますので、\(mg=-kx_0\)とデザイン変更されています。これを代入して
\(-m\omega^2 x=kx_0-kx_0-kx\)
\(m\omega^2=k\)
と式変形が続き、そのまま求めて行けそうです。
要は、鉛直ばね振り子を計算するときは、鉛直下向きを正にとって運動方程式を立てる方が簡単のようです。というか、問題設定を見てもらって、つり合いの点からずれた向きを正にとって立式する、ということです。今回の場合は、つり合いの点から、おもりを下に引っ張って考えている問題なので、鉛直下向き設定の方が簡単に解ける、ということです。
もし逆に、ばねを縮めてから手を放すような設定であれば、鉛直上向きを正とする方が簡単になると思います。
長くなりましたが、式変形を続けます。
\(m\omega^2=k\) より
\(\omega^2=\displaystyle \frac{k}{m}\)
\(\omega=\displaystyle\sqrt{\frac{k}{m}}\)
ここから周期を求めると、
\(T=\displaystyle\frac{2\pi}{\omega}\) より
\(T=2\pi \displaystyle\sqrt{\frac{m}{k}}\)
▼鉛直ばね振り子公式
角振動数
\(\omega =\displaystyle\sqrt{\frac{k}{m}}\)
周期
\(T=2\pi \displaystyle\sqrt{\frac{m}{k}}\)
つまり、水平のときと同じということです。重力加速度に関係しないので、無重力空間に持っていってもばねの上下運動に変化はないということですね。
加速度運動するエレベーター内で、慣性力を考慮するような問題が出たとしても、重力に関わる値が公式にありませんので、見かけの重力=慣性力についても、完全に無視して、水平ばね振り子として解くことができる点は、ずいぶんとお得な公式です。
