楕円
万有引力の単元に入る前に、楕円について学んでおきます。
楕円とは、円をつぶしたような形を表しています。円を作図するときには、コンパスで中心を決めて、中心からどの方位にも等しい距離で線をひいてやると描くことができますね。
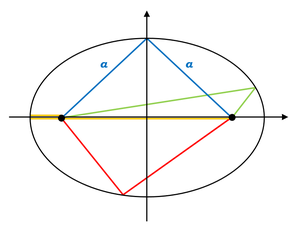
楕円を作図するときは、ある2か所に釘をとめて、この釘に糸をひっかけて、ペンでピンと糸を張り、ぐるっと一周させると描くことができます。このとき決めた2点を「楕円の焦点」と呼びます。
なので、図の青線で描いた線の長さは\(2a\)ですが、緑線の位置でもオレンジの線の位置でも赤線の位置でも、同じく\(2a\)の長さになっています。
楕円では、円と異なり、半径の長さが変わります。縦軸の一番短い半径を「短半径」、横軸の一番長い半径を「長半径」と呼びます。
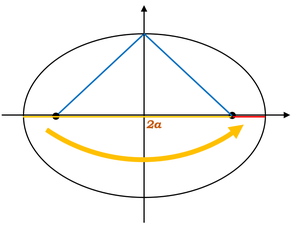
オレンジの線の長さが\(2a\)なので、左側の線が重なっている部分の長さを右に持ってくると、ちょうど横の直径の長さに相当することが分かりますね。
なので、この図の場合、長半径を\(a\)とすることができます。
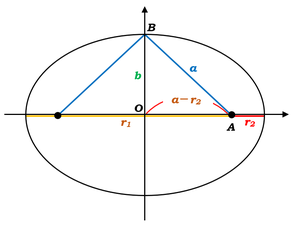
楕円の左端から右の焦点\(A\)までの距離を\(r_1\)、\(A\)から楕円の右端までの距離を\(r_2\)とします。
すると、\(OA\)は\(a-r_2\)とすることができますね。
また、\(r_1\)、\(r_2\)を置いた時点で、\(2a=r_1+r_2\)という関係式も表せます。
ここに現れる直角三角形\(OAB\)について、三平方の定理を使うと、
\(a^2=b^2+(a-r_2)^2\)
\(a^2=b^2+a^2-2ar_2+r_2^2\)
\(0=b^2-2ar_2+r_2^2\)
\(2a=r_1+r_2\) なので
\(0=b^2-(r_1+r_2)r_2+r_2^2\)
\(0=b^2-r_1r_2\)
\(b^2=r_1r_2\)
\(b=\sqrt{r_1r_2}\)
と式変形を追うことができます。
▼楕円の半径
楕円の左端から1つの焦点までの距離を\(r_1\)、そこから右端までの距離を\(r_2\)としたとき、
長半径\(a\):相加平均の形
\(a=\displaystyle\frac{r_1+r_2}{2}\)
短半径\(b\):相乗平均の形
\(b=\sqrt{r_1r_2}\)
