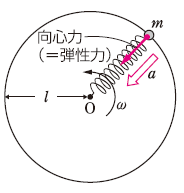
この問題で最初に引っかかるのは、回転させていくごとに小球に遠心力がかかって、どんどん半径が変わるんじゃないか、半径が長くなったら速さも角速度もかわるんじゃないか、という疑問を抱くところかと思います。
でも、そんな難しい設定ではありません。確かに、静止しているところからすべての運動を説明しようとすれば、「等角加速度回転運動」という難しい議論になりますが、これはすでに回転が安定して、バネがいくらか伸びて長さが一定になり、小球の速さも一定になり、等速円運動している状態からの問題です。
そこが腑に落ちれば、もはやなんてことない問題です。
(1)
\(a=r\omega^2\) より
\(a=l\omega^2[m/s^2]\)
向きは点\(O\)へ向く向き
問題文に単位が書いてあるので、解答の単位忘れに注意。
(2)
\(F=mr\omega^2\) より
\(F=ml\omega^2[N]\)
単位忘れに注意
(3)
向心力の正体は、ばねが小球を引く力ですので、向心力を書くとき、向心力の公式を使わなくても、フックの法則から式を示してあげることもできます。そうすると、ばねの自然長が\(l_0[m]\)、伸びたときの長さが\(l[m]\)なので、
\(F=kx\) より
\(F=k(l-l_0)[N]\)
と書くことができます。表現が違うだけで、その値は向心力と同じはずですから、
\(k(l-l_0)=ml\omega^2\)
とつなげることができます。よってばね定数は、
\(k=\displaystyle\frac{ml\omega^2}{l-l_0}[N/m]\)
