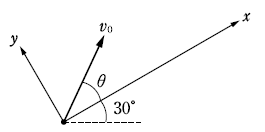
斜面に向かって斜方投射する問題を解くときには、ざっくり2パターンの解き方があります。
① 斜面を直線ととらえて、斜方投射の式と連立して、交点を数学的に求める方法
② 斜面を軸ととらえて、重力を軸方向に分解して、両軸とも等加速度運動であると物理学的に求める方法
今回は、すでに斜面が新しい軸に取り直されているので、②の方法で解き進めることにします。
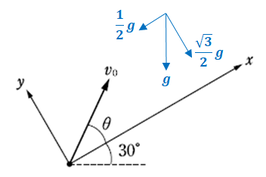
まず、初期設定として、重力加速度が斜め向きだと解釈して、問題文に与えられた軸の方向に分解します。
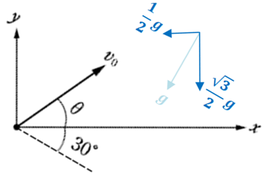
図を回転させて、\(x\)軸と\(y\)軸が、ノートの縦横の向きと同じ向きになるようにしてやると、とたんに見やすくなりますね。
実際のテストのときにも、問題用紙を回転させて眺めてみる方が分かりやすくなると思います。
見ての通り、両軸方向ともに加速度がありますので、どちらの軸も等加速度運動で解いてやる必要があります。
(1)
まず初速度を分解します。これはおなじみ。
水平初速度 \(v_{0x}=v_0cos\theta\)
鉛直初速度 \(v_{0y}=v_0sin\theta\)
ですね。
そして、先ほどの図で分解したように、加速度のそれぞれの成分は、
水平加速度 \(a_x=-\displaystyle\frac{1}{2}g\)
鉛直加速度 \(a_y=-\displaystyle\frac{\sqrt{3}}{2}g\)
となっています。
そして、これらを、等加速度運動の速度公式に代入します。
\(v=v_0+at\) より
\(v_x=v_{0x}+a_xt\)
\(v_x=v_0cos\theta - \displaystyle\frac{1}{2}gt\)
\(v_y=v_{0y}+a_yt\)
\(v_y=v_0sin\theta-\displaystyle\frac{\sqrt{3}}{2}gt\)
代入している文字が複雑なだけで、やっていることは等加速度運動の速度の式に\(v_0\)と\(a\)を代入しただけです。
(2)
斜面と衝突するとき、\(y=0\)となればいいので、
\(y=\)\(v_0\)\(t+\displaystyle\frac{1}{2}\)\(a\)\(t^2\) より
\(0=\)\(v_0sin\theta\)\(・t_0-\displaystyle\frac{1}{2}・\)\(\displaystyle\frac{\sqrt{3}}{2}g\)\(・t_0^2\)
\(t_0≠0\)なので、両辺から割って、
\(0=\)\(v_0sin\theta\)\(-\displaystyle\frac{1}{2}・\)\(\displaystyle\frac{\sqrt{3}}{2}g\)\(・t_0\)
\(\displaystyle\frac{1}{2}・\frac{\sqrt{3}}{2}g・t_0=v_0sin\theta\)
\(\displaystyle\frac{\sqrt{3}g}{4}・t_0=v_0sin\theta\)
\(t_0=\displaystyle\frac{4v_0sin\theta}{\sqrt{3}g}\)
(3)
水平方向にも等加速度運動しています。斜面に衝突するときの時刻は(2)で求めた\(t_0\)なので、
\(x=\)\(v_0\)\(t\)\(+\displaystyle\frac{1}{2}\)\(a\)\(t^2\) より
\(R=\)\(v_0cos\theta\)\(・t_0\)\(-\displaystyle\frac{1}{2}・\)\(\displaystyle\frac{1}{2}g\)\(・t_0^2\)
\(R=\)\(v_0cos\theta\)\(・t_0\)\(-\displaystyle\frac{g}{4}\)\(・t_0^2\)
\(R=\)\(v_0cos\theta\)\(・\displaystyle\frac{4v_0sin\theta}{\sqrt{3}g}\)\(-\displaystyle\frac{g}{4}\)\(・\displaystyle\frac{16v_0^2sin^2\theta}{3g^2}\)
\(R= \displaystyle\frac{4v_0^2sin\theta cos\theta}{\sqrt{3}g}-\displaystyle\frac{4v_0^2sin^2\theta}{3g}\)
\(R= \displaystyle\frac{4\sqrt{3}v_0^2sin\theta cos\theta}{3g}-\displaystyle\frac{4v_0^2sin^2\theta}{3g}\)
\(R= \displaystyle\frac{4v_0^2sin\theta}{3g}(\sqrt{3}cos\theta -sin\theta)\)
(4)
小球が斜面に対して垂直に衝突するのは、\(x\)軸方向の速度が\(0\)となったタイミングです。
なので(1)から、
\(v_x=v_0cos\theta - \displaystyle\frac{1}{2}g\)\(t_0\)
の式を持ってきて、\(v_x=0\)としておいて、(2)の、衝突時間 \(t_0=\displaystyle\frac{4v_0sin\theta}{\sqrt{3}g}\) を代入すると、
\(0=v_0cos\theta - \displaystyle\frac{1}{2}g・\)\(\displaystyle\frac{4v_0sin\theta}{\sqrt{3}g}\)
\(0=v_0cos\theta - \displaystyle\frac{4v_0sin\theta}{2\sqrt{3}}\)
\(0=cos\theta - \displaystyle\frac{4\sqrt{3}sin\theta}{2・3}\)
\(cos\theta = \displaystyle\frac{2\sqrt{3}sin\theta}{3}\)
\(\displaystyle\frac{sin\theta}{cos\theta}=\frac{3}{2\sqrt{3}}\)
よって
\(tan\theta=\displaystyle\frac{\sqrt{3}}{2}\)
