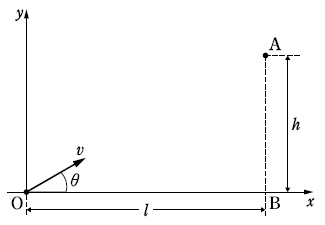
モンキーハンティングの問題です。
難しそうに見えますが、応用40と同じく、2物体の落体問題のシリーズですので、斜方投射と自由落下が1問に融合されたので応用になっていると思っておきましょう。順にたどるとそんなに難しくないはずです。
(1)
初速度\(v\)を分解しましょう。
水平初速度が \(v_x=vcos\theta\)
鉛直初速度が \(v_y=vsin\theta\)
ですね。
この問題では、まず弾丸が\(l\)の地点に到達するのがいつのころのことなのかを先に求めておいて、その時間での高さを求めれば、答えに到達できます。
\(x=vt\) より
\(l=vcos\theta×t\)
\(t=\displaystyle\frac{l}{vcos\theta}\)
これを斜方投射の高さの式に代入します。弾丸の高さを\(y_B\)として、
\(y=v_0\)\(t\)\(-\displaystyle\frac{1}{2}g\)\(t^2\) より
\(y_B=vsin\theta×\)\(\displaystyle\frac{l}{vcos\theta}\)\(-\displaystyle\frac{g}{2}\)\(\displaystyle\frac{l^2}{v^2cos^2\theta}\)
\(y_B=\displaystyle\frac{lsin\theta}{cos\theta}-\frac{gl^2}{2v^2cos^2\theta}\)
\(y_B=ltan\theta - \displaystyle\frac{gl^2}{2v^2cos^2\theta}\)
ここでの数式の物理的な意味も確認しておきましょう。
第一項は\(tan\theta\)に関する項で、重力がなければ斜め上向きに直線運動をします、という意味の式です。
第二項は\(g\)に関する項で、どれだけ落下するか、を意味する式です。
(2)
弾丸が命中するためには、当然、斜方投射された弾丸は横にちょうど\(l\)だけ進んでいるはずです。
そして、そこに到達するまでに要する時間は、
\(t=\displaystyle\frac{l}{vcos\theta}\)
であることを前で求めています。
あとは、自由落下してくる物体(モンキーの方)が、この時間でどの高さにいるのかを求め、その高さと弾丸の高さが一致するようにしてやれば、弾丸はモンキーに当たったことになりますね。
モンキーの高さは、弾丸と同じく鉛直上向きを正に取って考えます。符号に注意。
また、原点は弾丸の方に設定したので、モンキーは \(t=0\) のときにすでに初期高さ\(h\)にあることも注目しておきます。
モンキーの高さを\(y_A\)として、
\(y=-\displaystyle\frac{1}{2}gt^2+y_0\) より
\(y_A=-\displaystyle\frac{g}{2}×\)\(\displaystyle\frac{l^2}{v^2cos^2\theta}\)\(+h\)
\(y_A=-\displaystyle\frac{gl^2}{2v^2cos^2\theta}+h\)
弾丸が命中するとき、\(y_A=y_B\)なので、
\(ltan\theta - \displaystyle\frac{gl^2}{2v^2cos^2\theta}=-\frac{gl^2}{2v^2cos^2\theta}+h\)
\(ltan\theta=h\)
\(tan\theta=\displaystyle\frac{h}{l}\)
モンキーにも弾丸にも等しい重力がかかっているため、両辺に同じ形が現れます。その結果、どちらの式からも重力の要素が消えます。残った式の形は、重力がなかったとすると、弾丸の軌道は直線\(OA\)上を移動する、ということを意味しています。
なお、この問題では、\(tan\theta\)を求めよ、という指示にはなっていないので、\(ltan\theta=h\)で止めても、各文字の間の関係性は示せていますので、正解です。
(3)
\(tan\theta=\displaystyle\frac{h}{l}\) なので、問題の図の中に直線\(OA\)を描いてしまいましょう。
すると⊿\(OBA\)が作れますね。ここから、三平方の定理を使うと、
\(OA=\sqrt{l^2+h^2}\)
なので、
\(cos\theta=\displaystyle\frac{l}{\sqrt{l^2+h^2}}\)
これを、前で求めた時間の式に代入すると、
\(t=\displaystyle\frac{l}{vcos\theta}\) より
\(t=\displaystyle\frac{l}{v}×\)\(\displaystyle\frac{1}{cos\theta}\)
\(t=\displaystyle\frac{l}{v}×\)\(\displaystyle\frac{\sqrt{l^2+h^2}}{l}\)
\(t=\displaystyle\frac{\sqrt{l^2+h^2}}{v}\)
(4)
いま求めたのが、弾丸が衝突する時間です。では、実際に衝突したときの高さはいくらでしょう。それを求めて、その高さが\(>0\)であれば、地面より上で命中したことになりますね。
衝突したとき、\(y_A=y_B\)なので、どちらの式に代入してもいいですが、\(y_A\)の方が簡単そうなので、\(y_A\)に代入します。うまくいかないときは\(y_B\)に代入してみても同じ値に行きつくはずですよ。
\(y_A=-\displaystyle\frac{1}{2}gt^2+h\) より
\(y_A=h-\displaystyle\frac{1}{2}g・\) \(\displaystyle\frac{l^2+h^2}{v^2}\)
衝突した高さが地面より高ければいいので、
\(y_A>0\) より
\(h-\displaystyle\frac{g}{2}・\frac{l^2+h^2}{v^2}>0\)
\(h>\displaystyle\frac{g}{2}・\frac{l^2+h^2}{v^2}\)
\(hv^2>\displaystyle\frac{g}{2}・(l^2+h^2)\)
\(v^2>\displaystyle\frac{g(l^2+h^2)}{2h}\)
\(v>\sqrt{\displaystyle\frac{g(l^2+h^2)}{2h}}\)
