
(1)
ばね\(A\)と、ばね\(B\)は異なるばねですので、力を加えたときにどのくらい伸びるのかも異なります。
なので、一般的には、図のように吊り下げるとおもりは斜め向きになる可能性もありますが、この範囲ではまだおもりの大きさまで考慮しておらず、おもりには大きさがない質点として考えているのが前提に作問されています。
大きさがありませんので、おもりが斜めになることを考慮する必要はありませんし、何より、2つのばねが同じ長さだけ伸びる、としても良いことになります。
この問題で引っかかるとしたらその部分ですね。
伸びが同じである、ということが分かりさえすれば後は簡単です。図のように、それぞれのばねにかかる力を\(k_1x\)、\(k_2x\)としてやります。
おっと。図の矢印が逆ですね。間違えていました。ばね\(A\)にかかる力が\(k_1x\)で、ばね\(B\)にかかる力が\(k_2x\)です。
そしてそれらの和が重力とつり合うので、
\(k_1x+k_2x=mg\)
\((k_1+k_2)x=mg\)
\(x=\displaystyle\frac{mg}{k_1+k_2}[m]\)
となります。
(2)
\(k_1+k_2\)をまとめて1文字の\(k\)だとすると、2つのばねを1つのばねだとみなすことができますので、
\(k_並=k_1+k_2[N/m]\)
とできます。これを「並列合成ばね定数」と言います。
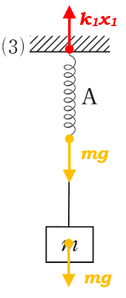
(3)
ばね\(A\)だけ考えると、ばね\(B\)がどれだけ伸びていようと関係なく、ばね\(A\)には重力\(mg\)が加わります。このときの伸びを\(x_1\)とすると、ばね\(A\)にかかる弾性力は\(k_1x_1\)と書くことができます。
このとき、
\(k_1x_1=mg\) より、ばね\(A\)ののびは
\(x_1=\displaystyle\frac{mg}{k_1}\)
です。
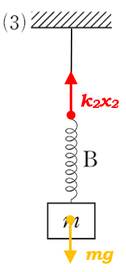
同様にばね\(B\)だけ考えると、ばね\(A\)がどれだけ伸びていようと関係なく、ばね\(B\)にはやはり重力\(mg\)のみが加わります。このときの伸びを\(x_2\)とすると、ばね\(B\)にかかる弾性力は\(k_2x_2\)と書くことができます。
このとき、
\(k_2x_2=mg\) より、ばね\(B\)ののびは
\(x_2=\displaystyle\frac{mg}{k_2}\)
です。
よって、ばねのトータルの伸びは、
\(x=x_1+x_2\)
\(x=\displaystyle\frac{mg}{k_1}+\frac{mg}{k_2}\)
\(x=mg・\left(\displaystyle\frac{1}{k_1}+\frac{1}{k_2}\right)\)
\(x=mg・\left(\displaystyle\frac{k_2}{k_1k_2}+\frac{k_1}{k_2k_1} \right)\)
\(x=mg・\displaystyle\frac{k_1+k_2}{k_1k_2}[m]\)
となります。
(4)
\(x=mg・\displaystyle\frac{k_1+k_2}{k_1k_2}\) より
\(\displaystyle\frac{k_1k_2}{k_1+k_2}x=mg\)
としてやると、
\(\displaystyle\frac{k_1k_2}{k_1+k_2}\)
の部分をまとめて\(k\)とすれば、ばね1つ分だとみなすことができそうですね。なので、
\(k_直=\displaystyle\frac{k_1k_2}{k_1+k_2}[N/m]\)
として表現します。これを「直列合成ばね定数」と言います。
