(1)
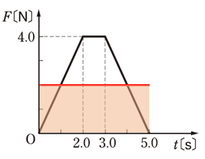
グラフの面積が力積を表します。
面積の計算の仕方は、台形の面積公式を使ってもいいですし、\(3.0s\)から\(5.0s\)までの三角形を切り取って\(0s\)から\(2.0s\)の方に移動させて長方形の面積として考えてもいいですね。自分の慣れた方法で、すぐに求まると思います。
(面積)\(=12N・s\)
(2)
面積が\(12N・s\)だということが求まりましたが、\(0s\)~\(5.0s\)までの間、ずっと同じ力が加わっていたと仮定します。このときの力のことを平均の力と呼びます。この平均の力はいくらでしょうか、という問題です。
面積\(12N・s\)がすでに求まっていて、横が\(5s\)ですので、わり算してやると、
\(\bar F =12÷5=2.4N\)
(3)
忘れがちなことですが、グラフで求まるのは、力積だけです。
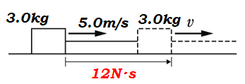
この問題の本来の部分は、質量\(3.0kg\)の物体が\(5.0m/s\)で運動していて、ここにグラフで求めた力積\(12N・s\)が加わることで物体の速度が速くなる、という設定です。
グラフで求まったのは、あくまでも、すでに運動している物体に、追加で\(12N・s\)の力積を加えてやった、という情報だけですので、
(元の運動量)+(加えた力積)=(あとの運動量)
の公式にそれぞれ代入してやって、力積を加えたあとの速度が一体いくらになるのか導出しましょう。
\(3.0[kg]×5.0[m/s]\) \(+12[N・s]\) \(= 3.0v'\)
\(15\) \(+12\) \(= 3v'\)
\(3v'=27\)
\(v'=9.0[m/s]\)
と求まりました。
