
(1)
平面の運動量問題のステップに従って解いていきましょう。
\(Step1\):運動量を表す矢印を同じ点から作図する
ここではラクをしたいので、図のボールを原点としてボールから2本の矢印を描くことにします。
皆さんが解くときは、この図のように解いてもいいですし、新たに別の所に同じ始点を持つ矢印を描いてもいいですね。
運動量の大きさも書き込んでおきましょう。
\(p=mv\) より
\(p=0.15[kg]×30[m/s]=4.5[kg・m/s]\)
ですので、両方の矢印の近くに書き込んでおきます。

\(Step2\):衝突前の運動量の矢印の先から、衝突後の運動量の矢印の先に線を引く
引いた線が加えた力積を表していますので、この矢印の向きと大きさを求めてやれば解答終了となります。
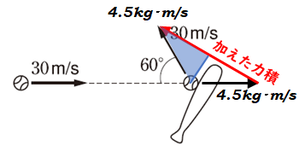
余弦定理を使って直接求めてもいいですが、余弦定理を使いこなせる数学力がある人は、おそらくこの解説ページには来ていないでしょう。
ボールから力積の矢印の線に向かって垂線を引きます。すると、図の青い直角三角形が表れ、これがちょうど\(1:2:\sqrt{3}\)の比の三角形になっています。
垂線の部分を\(1\)とすると、運動量が\(2\)、力積の矢印の半分が\(\sqrt{3}\)になりますね。ということは、
運動量:加えた力積 \(= 2:2\sqrt{3} = 1:\sqrt{3}\)
という比の関係が成立します。つまり、
運動量 \(×\sqrt{3} =\) 加えた力積
ということですので、
加えた力積\(I=4.5\sqrt{3}\)
\(≒4.5×1.73\)
\(=7.785≒7.8[N・s]\)
と求まりました。
(2)
力積の公式は \(I=F\Delta t\) です。
いま、問題文より\(\Delta t=1.0×10^{-2}[s]\)で、力積は(1)から\(I=7.8[N・s]\)だと求まっています。
それぞれ代入すると、
\(7.8=F×10^{-2}\)
\(F=7.8×10^2[N]\)
となりました。
