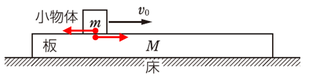
この問題は、リード物理基礎の応用86と同じ設定の問題ですね。
応用86では、それぞれ運動方程式を立てて、それぞれの加速度を求めさえすれば、等加速度公式に代入することで、どの時刻に一体化(小物体と板が同じ速度で動く状態)が完了するかを求めることができますよ、という問題でした。
問題に入る前に、この応用86の導出過程を、公式のままで追ってみます。
\(ma=F\)より \(a=\displaystyle\frac{F}{m}\)
これを等加速度公式 \(v=v_0+at\) に代入
\(v=v_0+\displaystyle\frac{F}{m}t\)
\(v-v_0=\displaystyle\frac{F}{m}t\)
\(mv-mv_0=Ft\)
となりました。つまり、応用86は運動量と力積の関係を使えば、運動方程式を解く操作を省略することができるわけです。
応用86を解く時点では、運動方程式しか解くワザを持っていませんでしたので、応用問題の区分でしたが、この章に到達した今となっては、運動量と力積が使えますから、レベルは基本問題まで降りてくるんですね。
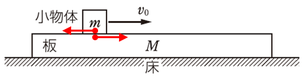
(1)
「小物体が板に対して静止した」というのは、「板に小物体が衝突し、一体化した」ということと同じ状態です。
衝突の仕方はおいといて、結局のところは、静止している板に運動している小物体が力を加えて、やがて同じ速さになる、ということなので、一体化問題として解きましょう。
ちなみに、加わっている力は、きちんと説明すれば、大きさ\(\mu mg\)の動摩擦力です。図のように加わります。
\(mv_0=(M+m)V\) より
\(V=\displaystyle\frac{mv_0}{M+m}\)
一体化問題だと読み解くことができさえすれば、解答部分は少ないですね。
(2)
時間についても問われたら、力積を使うのがスマートです。
板と小物体のどちらで考えてもいいですが、板の初速度が\(0\)なので、板で考えてみることにしてみましょうか。
方針としては、板についてだけで考えて、
(はじめの運動量)+(加えられた力積)=(あとの運動量)
という関係です。それぞれ文字で書くと、
\(0\) \(+ F\Delta t\) \(= MV\)
となります。板についてだけ考えていますので、あとの運動量は一体化したときの\((M+m)V\)ではありません。
力は動摩擦力\(F=\mu mg\)なので、
\(\mu mg t =M・\displaystyle\frac{mv_0}{M+m}\)
\(\mu g t =\displaystyle\frac{Mv_0}{M+m}\)
\(t = \displaystyle\frac{Mv_0}{\mu (M+m)g}\)
