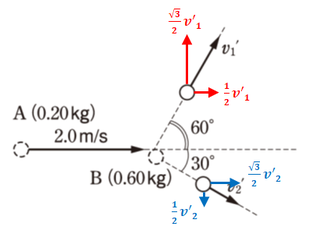
平面の衝突の問題のとき、運動量保存則は\(x\)軸と\(y\)軸のそれぞれで成立します。なので、\(v'_1\)と\(v'_2\)をそれぞれ縦と横に分解しておきましょう。
図の右向きを\(x\)軸の正、図の上向きを\(y\)軸の正ということにしておいて、それぞれの軸で運動量保存則を立てて計算してみましょう。
[\(x\)軸方向]
\(0.20[kg]×2.0[m/s] =\) \(0.20[kg]×\displaystyle\frac{1}{2}v'_1\) \(+ 0.60[kg]×\displaystyle\frac{\sqrt{3}}{2}v'_2\)
[\(y\)軸方向]
\(0 =\) \(0.20[kg]×\displaystyle\frac{\sqrt{3}}{2}v'_1\) \(- 0.60[kg]×\displaystyle\frac{1}{2}v'_2\)
それぞれ両辺\(2\)倍して、式を整理すると、
[\(x\)] \(0.8=0.2v’_1+0.6\sqrt{3}v'_2\)
[\(y\)] \(0=0.2\sqrt{3}v'_1-0.6v'_2\)
両辺\(10\)倍して小数も飛ばしておきましょう。
[\(x\)] \(8=2v’_1+6\sqrt{3}v'_2\)
[\(y\)] \(0=2\sqrt{3}v'_1-6v'_2\)
\(x\)の式を\(\sqrt{3}\)倍します。
[\(x\)] \(8\sqrt{3}=2\sqrt{3}v’_1+18v'_2\)
[\(y\)] \(0=2\sqrt{3}v'_1-6v'_2\)
辺々ひくと
\(8\sqrt{3}=24v'_2\)
\(v'_2=\displaystyle\frac{\sqrt{3}}{3}≒0.58m/s\)
上の\(y\)の式に代入すると
\(0=2\sqrt{3}v'_1-6×\displaystyle\frac{\sqrt{3}}{3}\)
\(0=v'_1-1\)
\(v'_1=1.0m/s\)
となりました。計算は一例ですので、連立式を立ててしまいさえすれば、好きな方法で解いてください。
