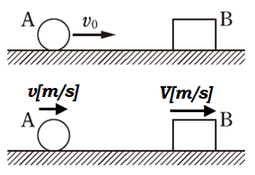
(1)
衝突後の速度が両方とも分からない場合、未知数\(2\)つに対して、運動量保存則の式\(1\)つでは解答まで到達できないのが目に見えています。
こういうとき、もう一本の式をどこから持ってくるのか、というと、反発係数の式との連立になります。
「運動量保存則と反発係数の連立」は、衝突問題のパターンの一つなので、知っておくと便利ですよ。
衝突後の速さが両方とも分からないときに使う解法パターンです。
衝突後、物体\(B\)は明らかに右に進みますが、小球\(A\)は右に進むのか左に進むのか分かりません。なので、符号がややこしくないように、とりあえず右向きに動くと仮定して文字を置いておきます。解答がマイナスになれば左向きだった、というだけですので、変に符号で悩まないようにするために、右向きにしておきましょう。
はじめ物体\(B\)は動いていないので、運動量はありません。
運動量保存則より、
\(mv_0=mv+MV\)
反発係数の式より
\(e=\displaystyle\frac{遠ざかる速さ}{近づく速さ}\)
\(e=\displaystyle\frac{V-v}{v_0}\)
これらを連立します。反発係数の式から
\(ev_0=V-v\)
\(V=v+ev_0\)
これを運動量保存則に代入すると、
\(mv_0=mv+M(v+ev_0)\)
\(mv_0=mv+Mv+eMv_0\)
\(mv_0=(M+m)v+eMv_0\)
\(mv_0-eMv_0=(M+m)v\)
\((M+m)v=(m-eM)v_0\)
\(v=\displaystyle\frac{m-eM}{M+m}v_0\)
反発係数の式 \(V=v+ev_0\) に代入すると
\(V=\displaystyle\frac{m-eM}{M+m}v_0+ev_0\)
\(V=\displaystyle\frac{m-eM}{M+m}v_0+\frac{e(M+m)}{M+m}v_0\)
\(V=\displaystyle\frac{m-eM+eM+em}{M+m}v_0\)
\(V=\displaystyle\frac{(1+e)m}{M+m}v_0\)
となりました。
(2)
小球\(A\)がはね返るということは、\(v<0\)であることを意味しますね。
\(v\)はすでに求まっていますので、
\(v=\displaystyle\frac{m-eM}{M+m}v_0<0\)
つまり
\(m-eM<0\)
\(m<eM\)
\(\displaystyle\frac{m}{M}<e\)
となります。一方で、反発係数にはもともと
\(0≦e≦1\)
という条件もありますので、これらの共通領域である
\(\displaystyle\frac{m}{M}<e≦1\)
が最終解答です。
