(1)
\(v=f\lambda\) より
\(v=5.0[Hz]×10[cm]\)
\(v=50[cm/s]\)
なので、三平方の定理から
\(S_1A=25[cm]\)
を求めておいて、距離÷速さをすると、
\(t=25[cm]÷50[cm/s]=0.50s\)
となります。
距離も速さも同じ\([cm]\)単位にしてしまえば、計算ができるということから、わざわざ\([m]\)への変換をせずに式を終わらせてしまうのがコツですね。
(2)
\(2\)つの波源が同位相源なので、波源の垂直二等分線上にある点\(A\)に関しては、特に途中過程を書くことなく、強め合う、でいいですね。
点\(B\)に関しては、導出しておきましょう。\(S_1B=50[cm]\)を三平方の定理で前もって出しておきます。
\(S_1B-S_2B=50[cm]-40[cm]=10[cm]\)
波長も\(10[cm]\)なので、点\(B\)も強め合う点となります。
(3)
\(S_1C-S_2C=10[cm]\)なので、点\(C\)は強め合いの点が来ます。なので、時間とともに波源の振幅の\(2\)倍の振幅で激しく水面が上下している点です。その前提で、今この瞬間は山ですか?谷ですか?という問題が出されています。
この瞬間が山か谷かを判断するだけであれば、片方の波源の情報があれば十分でしょう。
例えば、\(S_2C\)について考えます。\(S_2C=15[cm]\)を波長\(10cm\)の波が進むので、\(S_2\)が山となるようにして\(S_2C\)間の波を作図してみます。すると、点\(C\)にはちょうど谷が来ます。強め合いの点なので、おそらく示さなくても\(S_1\)からの波も谷がくることでしょう。重ねあって大きな谷になるはずです。
よって、谷。
(4)
見慣れない問題ですが、聞かれていることは単純です。まず、波が\(0.30s\)でどの程度進むのか、ということを計算しておきます。
\(x=vt\) より
\(x=50[cm/s]×0.30[s]=15[cm]\)
これでほぼ終了です。
\(S_1C=25[cm]\)ですが、\(0.30s\)経過すると、さらに\(15cm\)進んで、\(S_1C'=40[cm]\)
\(S_2C=15[cm\)の方も、\(15cm\)進めると、\(S_2C'=30[cm]\)
となります。
この問題のうれしいところは、これでおしまいということです。\(S_1C'=40[cm]\)、\(S_2C'=30[cm]\)となるような点を示しなさい、という問題ではないので、移動した先がどこかということまでは問うていないんですね。
(5)
線分上の節や腹の数を求める問題は解き方がパターン化しています。
\(Step1\):波源と波源をつなぐ線分の中点に印をつける。
いま、同位相源なので、ここは強め合う点ということになります。
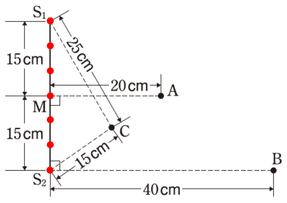
\(Step2\):\(\displaystyle\frac{1}{2}\lambda\)ごとに点をうつ
\(\lambda=10cm\)なので、\(5cm\)ごとに点を描けばいいですね。
節線間隔・腹線間隔は\(\displaystyle\frac{\lambda}{2}\)なので、これらすべて強め合う点となります。
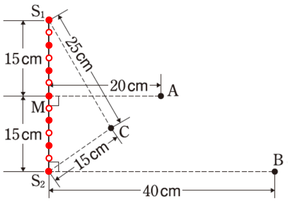
\(Step3\):打った点の間に別の印で点を打つ
この問題では、●を強め合う点としていますので、○は弱め合う点を表すことになりますね。この○印を通るように節線が描かれるはずですから、線分上の節の数が\(6\)個、節線は\(6\)本ということがわかります。
ちなみに腹線は\(7\)本ですね。\(S_1S_2\)間に\(5\)本と、波源からの半直線が上下にそれぞれ\(1\)本ずつです。
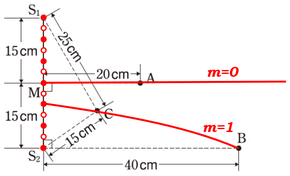
(6)
\(S_2M\)上に節が\(3\)個あるから、線分\(S_2B\)上にも節線が\(3\)本通る、という考えは早計です。直線\(S_2B\)上であれば\(3\)本通りますが、線分となると、必ずしもそうとは限りません。
点\(B\)がどのような点なのかを考えてみます。(2)で解いたように、
\(S_1B-S_2B=50[cm]-40[cm]=10[cm]\)
なので、点\(B\)は強め合う点です。しかも、この点、たまたま波長\(\lambda=10cm\)と一致する点なので、強め合いの条件式\(m\lambda\)でいうところの\(m=1\)となる点です。
\(2\)つの波源からの経路差\(=0\)のとき\(m=0\)、経路差\(=\lambda\)のとき\(m=1\)、経路差\(=2\lambda\)のとき\(m=2\)としていくのが強め合いの干渉の条件でしたね。
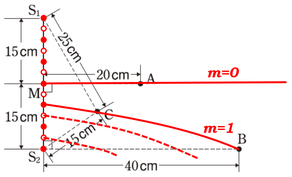
そうなると、線分\(S_2B\)上を通る節線は、図のように\(2\)本だけということになります。
\(m=0\)の節線は点\(B\)よりも右側を通りますので、「線分上」ではなくなりますね。
[補]
この問題は、たまたま点\(B\)が\(m=1\)の強め合いの点と重なったので説明がラクでした。ですが、一般的には点\(B\)が腹線上、あるいは節線上に来るとは限りません。
そういうときは、経路差を計算したときに、それが\(m\)イコールいくらになるのかで目算をつけて考えます。例えば、\(S_1B-S_2B=12cm\)だったとします。\(\lambda=10cm\)なので、干渉条件の「経路差\(=m\lambda\)」の式に無理やり入れると、\(m=1.2\)となります。
すると、点\(B\)がある場所は、\(m=1\)よりは大きいけど\(m=2\)よりはだいぶ\(m=1\)の線のほうに近いはずだ、のように想像することができますね。
そういうキリの悪い設定はあまり見かけないですが、解けなくはない問題です。
