■解答
(あ) \(\displaystyle\frac{\lambda}{n}\) (い) \(E_{R_0}=-pE sin 2 \pi \left( ft+ \displaystyle\frac{z}{\lambda}\right)\) (う) \(E_{T'_1}=qE sin 2 \pi \left(ft-\displaystyle\frac{nz}{\lambda}\right)\)
(えお) \(E_{R_1}=pqq'E sin [ 2 \pi (ft+\displaystyle\frac{z}{\lambda})-\frac{4 \pi nD}{\lambda}]\)
問1 \(A^2=p^2E^2(q^2q'^2-2qq'cos \phi -1)\)
(か) \(D=\displaystyle\frac{2m-1}{4n}\lambda\) (き) \(A=(1+qq')pE\) (く) \(D=\displaystyle\frac{m}{2n}\lambda\)
(け) \((1+p^2)qq'E\) (こ) \(D=\displaystyle\frac{2m-1}{4n}\lambda\) (さ) \((1-p^2)qq'E\)
問2 強め合うとき \(A^2=E^2\) 弱め合うとき \(A^2=\displaystyle\frac{1-p^2}{1+p^2}E\)
問3 薄膜\(X\)を用いるのが良い。 薄膜\(X\)は、\(p\)が\(1\)に近い値を持つものを用いると良い。
■解説
(あ) 屈折率\(n\)の薄膜に入射したので、
\(\displaystyle\frac{\lambda}{n}\)
(い) 入射光の電場の\(x\)成分は\(z<0\)において
\(E_Ⅰ=Esin 2 \pi \left( ft - \displaystyle\frac{z}{\lambda} \right) \)
で与えられているので、
① 反射光の振幅\(p\)倍
② 反射面で位相が逆転
③ 反射波の進行方向は元の逆向き
であることから、
\(E_{R_0}=\) \(\underset{②}{\underline{-}}\) \(\underset{①}{\underline{p}}\) \(E sin 2 \pi ( ft\)\(\underset{③}{\underline{+}}\)\( \displaystyle\frac{z}{\lambda})\)
(う) 同様に、透過光は、
① 透過光の振幅\(q\)倍
② 膜内波長 \(\displaystyle\frac{\lambda}{n}\)
であることから、
\(E_{T'_1}=\) \(\underset{①}{\underline{q}}\) \(E sin 2 \pi ( ft-\)\(\underset{②}{\underline{\displaystyle\frac{ z }{\frac{\lambda}{n}}}})\)
\(=qE sin 2 \pi (ft- \displaystyle\frac{nz}{\lambda})\)
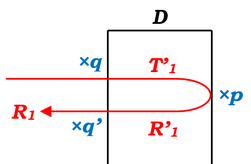
(えお) 同様に、
① \(z=0\)で透過して振幅\(q\)倍
② \(z=D\)で反射して振幅\(p\)倍
③ \(z=0\)で再び透過して振幅\(q'\)倍
④ 反射波の進行方向は元の逆向き
⑤ 膜内波長 \(\displaystyle\frac{\lambda}{n}\)
⑥ 膜内での波の通過距離が往復\(2D\)
であることから、
\(E_{R_1}=\) \(\underset{①②③}{\underline{qpq'}}\) \(E sin 2 \pi [ ( ft\) \(\underset{④}{\underline{+}}\)\(\displaystyle\frac{z}{\lambda})-\) \(\underset{⑤⑥}{\underline{\displaystyle\frac{ 2D }{\frac{\lambda}{n}}}}]\)
\(=\)\(pqq'\) \(E sin 2 \pi [ (ft\) \(+\)\(\displaystyle\frac{z}{\lambda})-\) \(\displaystyle\frac{2nD}{\lambda}]\)
\(=pqq'E sin [2 \pi ( ft + \displaystyle\frac{z}{\lambda})-\frac{4 \pi nD}{\lambda}]\)
問1 \(R_0\)光と\(R_1\)光の電場を重ね合わせると、
\(-pE sin 2\pi (ft +\displaystyle\frac{z}{\lambda} ) + pqq'E sin \left[ 2\pi (ft + \frac{z}{\lambda})-\frac{4 \pi n D}{\lambda} \right]\)
ここで
\(\theta≡2 \pi ( ft + \displaystyle\frac{z}{\lambda})\)
としておくと、
\(-pE sin \theta + pqq'E sin (\theta + \phi)\)
\(=-pE sin \theta + pE・qq'(sin \theta cos \phi + cos\theta sin \phi)\)
\(=pE \left[ sin \theta (qq' cos \phi -1) + qq' cos \theta sin \phi \right]\)
\(=pE \left[ (qq'cos\phi -1) ・sin\theta + qq'sin\phi・cos\theta \right] \)
ここに、\(asin\theta + bcos\theta =\sqrt{a^2+b^2}sin(\theta+\beta)\) を適用して、
\(=pE\sqrt{(qq'cos\phi-1)^2+(qq'sin\phi)^2} ・sin(\theta+\beta)\)
これを2乗すると、
\(p^2E^2\left[ (qq'cos \phi -1)^2+(qq'sin \phi)^2 \right] sin^2(\theta+\beta)\)
\(=p^2E^2\left[ (q^2q'^2 cos^2\phi-2qq'cos\phi +1) +(q^2q'^2sin^2\phi) \right] sin^2(\theta + \beta)\)
\(=p^2E^2(q^2q'^2-2qq'cos\phi +1) sin^2 (\theta+\beta) \)
であるから、光の強度(振幅の2乗(\(A^2\)))部分は、
\(A^2=p^2E^2(q^2q'^2-2qq'cos\phi -1)\)
(か) 光の強度が最大になるのは、\(cos\phi=-1\)となるときである。
よって
\(\phi=-\displaystyle\frac{4\pi nD}{\lambda}=(2m-1)\pi\) \((m=1,2,3…)\):問題文で指定されている
となるときであるが、\(cos\phi=cos(-\phi)\) より
\(\displaystyle\frac{4 \pi nD}{\lambda}=(2m-1)\pi\)
でも成り立つことから、
\(D=\displaystyle\frac{2m-1}{4n}\lambda\)
※この式は、\(2nD=(m-\frac{1}{2})\lambda (m=1,2,3…)\) と同義だということに気付けると意味が理解しやすいですね。
(き) このとき、光の強度は
\(A^2=p^2E^2(q^2q'^2+2qq'+1)\)
\(=(1+qq')^2p^2E^2\)
であるから、振幅は
\(A=(1+qq')pE\)
(くこ) 干渉条件より
[強め合うとき] \(2nD=m\lambda\) ⇔ \(D=\displaystyle\frac{m}{2n}\lambda\)
[弱め合うとき] \(2nD=(m-\frac{1}{2}\lambda)\) ⇔ \(D=\displaystyle\frac{2m-1}{4n}\lambda\)
(けさ) \(T_1\)光の振幅が\(qq'E\)、\(T_2\)の光の振幅が\(p^2qq'E\) であるから、
[強め合うとき] \(qq'E+p^2qq'E=(1+p^2)qq'E\)
[弱め合うとき] \(qq'E-p^2qq'E=(1-p^2)qq'E\)
問2
\(T_1\)光の振幅が \(qq'E\)
\(T_2\)光の振幅が \(p^2qq'E\)
\(T_3\)光の振幅が \(p^4qq'E\)
\(T_4\)光の振幅が \(p^6qq'E\)
\(…\)
と続くので、薄膜の厚さ\(D\)が\(\lambda\)の[ く ]倍のとき、つまり強め合うときは、
\(A=qq'E+p^2qq'E+p^4qq'E+p^6qq'E+…\)
\(=(1+p^2+p^4+p^6+…)qq'E\)
\(=\displaystyle \sum_{k=0}^{\infty} (p^2)^k・qq'E\)
\(=\displaystyle\frac{1}{1-p^2}qq'E\)
ここで、\(p^2+qq'=1\) ⇔ \(qq'=1-p^2\) より
\(\displaystyle\frac{1-p^2}{1-p^2}E=E\)
よって光の強度は \(A^2=E^2\)
一方で、薄膜の厚さ\(D\)が\(\lambda\)の[ こ ]倍のとき、つまり弱め合うときは、
\(T_1\)光と\(T_2\)光が逆位相
\(T_2\)光と\(T_3\)光が逆位相
\(T_3\)光と\(T_4\)光が逆位相
\(…\)
となれば良いので、
\(A=qq'E-p^2qq'E+p^4qq'E-p^6qq'E+…\)
\(=(1-p^2+p^4-p^6+…)qq'E\)
\(=\displaystyle \sum_{k=0}^{\infty} (-p^2)^k・qq'E\)
\(=\displaystyle\frac{1}{1+p^2}qq'E\)
同様に、\(p^2+qq'=1\) ⇔ \(qq'=1-p^2\) より
\(\displaystyle\frac{1-p^2}{1+p^2}E=E\)
よって光の強度は \(A^2=\left( \displaystyle\frac{1-p^2}{1+p^2}\right)^2E^2\)
問3 特定の波長の光を選択して抽出するには、対象となる波長以外の部分が\(0\)に近ければ良いので、
薄膜\(X\) を用いるのが良い。
このとき、弱め合う光の強度が\(0\)に近ければ良いので、薄膜\(X\)は、
\(p\)が\(1\)に近い 値を持つものを用いると良い。
