(1)
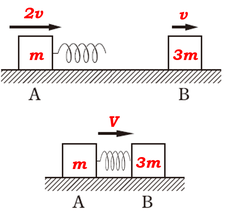
2つの相対速度が0となる、というのは、ばねが最大限まで縮んで、2つの物体が一体化している状態をいいます。その後この物体系は再び離れていきますが、(1)では最大限まで縮んだ瞬間のみを題材にしているので、その後のことは一旦おいておきます。
衝突前のそれぞれの運動量を求めて、その和を計算すると、
\(m×2v + 3m×v = 2mv+3mv = 5mv\)
衝突後、一体となっているときの運動量は、合計質量が\(4m\)で、速度を\(V\)としているので、
\(4mV\)
運動量保存則より
\(5mv=4mV\)
\(V=\displaystyle\frac{5}{4}v\)
(2)
同じような作業を、運動エネルギーでもやってみましょう。
衝突前のそれぞれの運動エネルギーを求めて、その和を計算すると、
\(\displaystyle\frac{1}{2}m・(2v)^2 + \frac{1}{2}・3mv^2\)
\(=\displaystyle\frac{4}{2}mv^2 + \frac{3}{2}mv^2\)
\(=\displaystyle\frac{7}{2}mv^2\)
衝突後の運動エネルギーは、
\(\displaystyle\frac{1}{2}・4mV^2\)
\(=\displaystyle\frac{1}{2}・4m・\left( \frac{5}{4}v \right)^2 \)
\(=\displaystyle 2m・\frac{25}{16}v^2\)
\(=\displaystyle\frac{25}{8}mv^2\)
この差\(\Delta K\)を求めると、
\(\Delta K = \displaystyle\frac{25}{8}mv^2-\frac{7}{2}mv^2\)
\(=\left( \displaystyle\frac{25}{8}-\frac{28}{8} \right) mv^2\)
\(=-\displaystyle\frac{3}{8}mv^2\)
(3)
運動エネルギーだけでなく、力学的エネルギー全体の保存を考えると、最初に持っていた運動エネルギーが、一体化しているときには、別の運動エネルギーと弾性エネルギーとの和になっていると考えることができます。
つまり、力学的エネルギー保存則より
初めの運動エネルギー = 後の運動エネルギー + 弾性エネルギー
という関係が成立しています。
そのうち、「後の運動エネルギー-初めの運動エネルギー」が\(\Delta K\)ですので、運動エネルギーが減った分はすべて弾性エネルギーになったと考えることができます。
そこで、符号に気をつけて、「減った分の運動エネルギー=弾性エネルギー」としてやって、
\(\displaystyle\frac{3}{8}mv^2=\frac{1}{2}kx^2\)
\(kx^2=\displaystyle\frac{3}{4}mv^2\)
\(x^2=\displaystyle\frac{3m}{4k}v^2\)
\(x=\displaystyle\frac{v}{2}\sqrt{\frac{3m}{k}}\)
\(4\)をルートの外に出し忘れないようにしましょう。物理は数学と違って、入っていても不正解にはならないとは思いますが、出てる方がきれいです。
