
(1)
棒の重さ、人の重さ、床にはたらく摩擦力、壁面がはしごを支える力をそれぞれ作図します。
摩擦力を作図するとき、向きに気をつけてください。仮に摩擦がなければどちらに動くかを考えて、それと逆向きに作図をします。
力のモーメント関連の問題は、解き方がパターン化されています。
鉛直方向、水平方向の力のつり合いの式と、力のモーメントの式の3本を連立すると、大概の問題は解けるように構成されています。
その方法を使って追っていきましょう。
[鉛直方向の力のつり合い]
\(mg+5mg=N_B\)
[水平方向の力のつり合い]
\(N_A=f\)
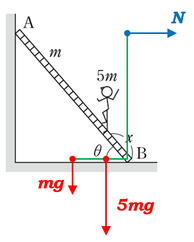
力のモーメントの式は、それぞれの力を棒に対して分解するよりも、この図の場合であれば力を作用線上で動かしてしまって、都合いい空中の場所に作図してしまう方がラクです。
力のモーメントの問題では、力の矢印は、その作用線上(矢印が向く直線上)であれば好きに動かしても解答はすべて同じになります。ただし、矢印の作用線上から外れると解答はズレますので、動かしすぎないように気をつけてください。
力のモーメントの計算をするときに、「力×長さ」を計算する都合上、力と長さが垂直な方が計算がラクです。そこで矢印をスライドさせた図が2つ目の図です。
これを利用しながら、点\(B\)周りの力のモーメントの式を立てていきましょう。
[点\(B\)周りの力のモーメント]
\(mg×\displaystyle\frac{l}{2}・\frac{3}{5} + 5mg・\frac{3}{5}x = N_A・\frac{4}{5}l\)
ここで、突如登場した\(\displaystyle\frac{3}{5}\)や\(\displaystyle\frac{4}{5}\)ですが、いま、\(tan\theta=\displaystyle\frac{4}{3}\)ですので、この三角形は\(3:4:5\)の三角形だということに気付きましょう。
\(tan\theta=\displaystyle\frac{4}{3}\)というのは、底辺が3、高さが4の三角形ですので、斜辺は5となります。
そこから、\(sin\theta\)も\(cos\theta\)も使わずに、三角比だけで求めています。
床の方の長さを求めるときは、はしごの長さの\(\displaystyle\frac{3}{5}\)倍、点\(B\)から\(N_A\)の作用線までの長さははしごの長さの\(\displaystyle\frac{4}{5}\)倍になっています。
おっと。図の\(N_A\)がただの\(N\)になっていますね。もう直すのめんどくさいので、このままにしときます。各自で\(A\)書き足しといてください。
これら3つの式を連立して解きます。
力のモーメントの式から、
\(\displaystyle\frac{3}{10}mgl + \frac{15}{5}mgx = \frac{4}{5}N_Al\)
\(N_A=f\)なので、文字を置き換えて、ついでにすべての式の分母をそろえてしまいましょうか。
\(\displaystyle\frac{3}{10}mgl + \frac{30}{10}mgx = \frac{8}{10}fl\)
両辺10倍して
\(3mgl + 30mgx = 8fl\)
\(3mg(l+10x)=8fl\)
よって
\(f=\displaystyle\frac{3mg(l+10x)}{8l}\)
計算過程は自由に進めればいいと思いますが、分母をそろえることで両辺10倍するのが見やすい形で変形できて計算ミスが減ります。
分母が簡単に揃えられるときは、こういう方法もコツの一つだと思っておいてください。
(2)
はしごがすべり出す直前、摩擦力\(f\)は最大静止摩擦力\(\mu N_B\)となっています。
すべり出すまでの摩擦力は単なる静止摩擦力なので、\(N_A=f\)以上の情報はなく、加えた力の分だけ作用反作用の法則が適用されるので、人がはしごをのぼることではしごが壁にギュッと押し付けられ、\(N_A\)が大きくなっていく分、摩擦力も次第に大きくなっていきます。ですから値はどんどん変化していきます。
しかし限界がくると、はしごはもはや床との摩擦だけでは支えられなくなるので、すべり出します。このときの摩擦が最大静止摩擦力で、この時の値だけ、いわゆる摩擦の公式が適用できます。摩擦の公式を何でもかんでも\(f=\mu N\)と覚えている人は、そこに知識の抜けがありますので注意してください。
\(f=\mu N\)は、静止できるギリギリ限界点のみで適用できる公式です。
さて(1)で求めた\(f\)に、その最大摩擦力の式を適用しましょう。
\(f=\displaystyle\frac{3mg(l+10x)}{8l}\) より
\(\mu N_B=\displaystyle\frac{3mg(l+10x)}{8l}\)
\(N_B\)は、鉛直方向の力のつり合いの式から即座に\(6mg\)と求まりますので、\(\mu=0.5\)とともに代入して、
\(0.5 ×6mg=\displaystyle\frac{3mg(l+10x)}{8l}\)
\(3mg=\displaystyle\frac{3mg(l+10x)}{8l}\)
\(1=\displaystyle\frac{l+10x}{8l}\)
\(8l=l+10x\)
\(10x=7l\)
\(x=\displaystyle\frac{7}{10}l\)
よって、点\(B\)から\(\displaystyle\frac{7}{10}l\)だけのぼった点
となります。
