
(1)
ここは素通りしましょう。重力を分解すると、図の通りです。
ア:\(mgsin\theta\)
イ:\(mgcos\theta\)
(2)
摩擦角の導出過程です。
斜面に沿って下方向には\(mgsin\theta\)がかかっていて、最大摩擦力はその逆向き(f=\mu N\)としてはたらきます。
\(N=mgcos\theta\)なので、代入した上で力のつり合いの式を立てると、
\(mgsin\theta_1=\mu mgcos\theta_1\)
\(sin\theta_1=\mu cos\theta_1\)
\(\displaystyle\frac{sin\theta}{cos\theta}=\mu\)
\(\mu =tan\theta_1\)
となります。このように、斜面上にある物体がすべり始めるときの角度を摩擦角といい、この公式自体は物体に大きさがあってもなくても成立します。
(3)
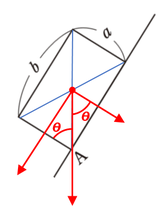
角度を急にしていくと、ちょうど重力の作用線が点\(A\)と重なるまでは何とか物体は斜面に張り付いていますが、これよりも角度を急にすると物体は回転してしまいます。
一般的に重力の作用線と面との交点を考えたとき、この交点が物体と斜面との接面にいるうちは回転しませんが、物体と斜面との接面から外れると、もはや斜面が物体を支えることができなくなります。
この問題で重要になるのは、\(\theta\)の取り方です。図のように、重力の作用線が点\(A\)と重なるように作図したとします。ここで、なかなか\(\theta\)がうまく取れない人が多いですので、たどり方を確認してみましょう。
(1)で作図したように、まずは重力を素直に分解します。このときの\(\theta\)をどこに取っていたかを間違えずに作図します。\(\theta\)の場所が分からなくなったときは\(\theta=10°\)くらいの図をいったん作図すると、どこに\(\theta\)を書くべきか、取り違えることは無くなると思います。
そして、図のように平行線における錯角を利用すると、角\(A=\theta\)を作図することができます。
ここまで来たら終了ですね。あとは、その角を三角比で表すことになります。一般的には\(tan\theta\)を使って表現するのがいいでしょう。
\(tan\theta_2=\displaystyle\frac{b}{a}\)
(4)
ここまでの話で、滑らないためには\(tan\theta<\mu\)、回転するためには\(\tan\theta>\displaystyle\frac{b}{a}\)となります。不等号の取り方が分からない人は、\(tan\theta\)を単なる傾きだと読み替えてください。滑らないためには傾きは小さくあるべきです。回転するためには傾きは大きくあるべきです。
これらの共通領域を取ってやると、
\(\displaystyle\frac{b}{a}<tan\theta<\mu\)
となりますので、
\(\displaystyle\frac{b}{a}<\mu\)
が成立していなければならないということです。
