(1)
単なる落体の問題です。落下時間を\(t\)とすると、高さ\(h\)だけ落下するのに要する時間は、
\(h=\displaystyle\frac{1}{2}gt^2\) より
\(t^2=\displaystyle\frac{2h}{g}\)
\(t=\displaystyle\sqrt{\frac{2h}{g}}\)
このときの質点の速さは
\(v=gt\) より
\(v=g・\displaystyle\sqrt{\frac{2h}{g}}\)
\(v=\sqrt{2gh} [m/s]\)
として求まります。ですが、等加速度運動の問題で時間が問題文に与えられていないときには、\(v^2-v_0^2=2ax\)の公式を使った方が早く計算できるんでしたね。
この公式を使うと、\(v_0=0\)ですから、
\(v^2=2gh\)
\(v=\sqrt{2gh} [m/s]\)
と、すぐに答えまで到達できます。確かに便利なのは便利でしょう。でも、この公式を覚えていなければ使えません。残念ながら3つ目の公式を覚えている人は少数派です。では、そんな人たちはどう対処するといいでしょうか。
等加速度運動の3つ目の公式を覚えていない人は、ここまで学習したのであれば、力学的エネルギー保存則が使えます。質点の質量を\(m\)として、
\(mgh=\displaystyle\frac{1}{2}mv^2\)
\(gh=\displaystyle\frac{1}{2}v^2\)
\(v^2=2gh\)
\(v=sqrt{2gh} [m/s]\)
これだと、式は少しだけ長いですが、落下時間を求めるほどではないですし、何より覚えている公式から解決させることができるので、都合がいい人が多いのではないでしょうか。
別解を3つほど示しました。好きな方法で解きましょう。
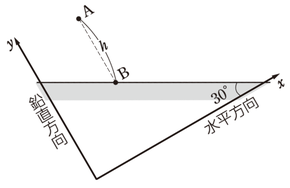
(2)
衝突する面が斜めなのが分かりにくいですので、図を少しだけ回転させて、見やすい向きにしておきます。

ここに質点が衝突していきますが、いま、弾性衝突なので、速さの成分は一切変化することなく、ちょうど光が鏡に当たったときのように、入射角=反射角となって飛び出していきます。
ここでは入射角も反射角も\(30°\)になりますね。
仮に、弾性衝突でなければ、面に対して垂直な速度成分だけが反発係数\(e\)倍されますし、仮に、床に摩擦係数\(\mu\)の摩擦があれば、面に対して水平な速度成分だけが、衝突に要した一瞬の時間\(\Delta t\)だけ力積\(f \Delta t\)をうけて遅くなります。
これらのややこしい話は、今はナシとなっています。
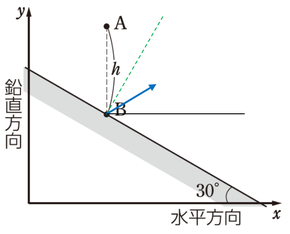
図をもとの向きに戻して、はね返った後の速度の矢印だけにしておきます。
合わせて、\(x\)軸と平行な補助線を点\(B\)から引いておきます。
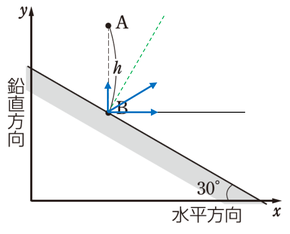
そして、改めて\(x\)軸と\(y\)軸の向きに速さを分解してやって、これらの成分をそれぞれ求めましょう。
[\(x\)軸成分]
\(v_x=v×\displaystyle\frac{\sqrt{3}}{2}\)
\(v_x=\sqrt{2gh}×\displaystyle\frac{\sqrt{3}}{2}\)
\(=\displaystyle\sqrt{\frac{3gh}{2}} [m/s]\)
[\(y\)軸成分]
\(v_y=v×\displaystyle\frac{1}{2}\)
\(v_y=\sqrt{2gh}×\displaystyle\frac{1}{2}\)
\(=\displaystyle\sqrt{\frac{gh}{2}} [m/s]\)

(3)
運動量の変化から力積を求めるときは、
\(step1\):運動量の矢印を同じ点から作図する
\(step2\):衝突前の運動量の矢印の先から、衝突後の矢印の先に線をひく
\(step3\):作図した矢印の長さを求める
の手順で求めます。
作図したものを載せておきます。見やすくするために斜面が水平になるようにずらしてあります。
作図してみると、別に正弦定理や余弦定理を使うことなく、\(1:2:\sqrt{3}\)の三角比のみからで計算ができそうなことが分かります。
辺の比を考えると、衝突前もしくは衝突後の質点の運動量の\(\sqrt{3}\)倍の値を求めてやれば良さそうです。
質点の運動量は
\(p=mv\) より
\(p=m\sqrt{2gh}\)
なので、その\(\sqrt{3}\)倍は
\(p=m\sqrt{6gh} [N・s]\)
となりました。
