■解答
問1 \(v_B=\sqrt{2gh}\) 問2 \(h_0=\displaystyle\frac{R}{2}\) 問3 (あ)
問4 \(v_D=\displaystyle\frac{4}{3}v_C\cos\theta\) 問5 \(\displaystyle\frac{L}{2}\) 問6 \(\displaystyle\frac{7}{6}L\)
問7 \(t_s=\displaystyle\frac{4v_C\cos\theta}{3\mu g}\) 問8 \(t=1-\displaystyle\sqrt{1-\frac{9\mu gx}{8v_C^2\cos^2\theta}}\)
問9 \(\left( 1+\displaystyle\frac{\cos^2\theta}{3} \right) mg(2R+h)\)
■解説
問1
点\(B\)を高さの基準として、力学的エネルギー保存則を立てると
\(mgh=\displaystyle\frac{1}{2}mv_B^2\)
\(v_B=\sqrt{2gh}\)
問2
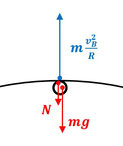
点\(B\)における力のつり合いの式は、
\(m\displaystyle\frac{v_B^2}{R}=N+mg\)
小物体が円周から離れることなく運動するためには、\(N≧0\) でなければならない。つまり、
\(m\displaystyle\frac{v_B^2}{R}≧mg\) (遠心力≧重力)
でなければならないということです。
ここに問1の結果を代入すると、
\(m\displaystyle\frac{2gh}{R}≧mg\)
\(h≧\displaystyle\frac{R}{2}\)
なので、\(h\)の最小値\(h_0\)は、等号成立のときです。つまり、
\(h_0=\displaystyle\frac{R}{2}\)
問3
2つの物体は、それぞれ自由落下と水平投射運動となります。よって、両者の落下時間は等しいので、(あ)。
問4
分裂直前の点\(D\)での速度を\(V\)とすると、点\(C\)での速度の水平成分と等しいので、
\(V=v_C\cos\theta\)
となります。また、点\(D\)での分裂前後の運動量保存則より
\(mV=0+\displaystyle\frac{3}{4}mv_D\)
よって
\(v_C\cos\theta=\displaystyle\frac{3}{4}v_D\)
\(v_D=\displaystyle\frac{4}{3}v_C\cos\theta\)
となります。
問5
軽い物体は、分裂後に速度がゼロになるので、自由落下を行います。
よって、
\(\displaystyle\frac{L}{2}\)
問6
\(V=\displaystyle\frac{3}{4}v_D\) より
\(v_D=\displaystyle\frac{4}{3}V\) なので、
点\(C\)から点\(D\)までに要する時間を\(t\)とすると、点\(D\)から地面までの落下に要する時間も\(t\)となります。
点\(C\)における速度の水平成分と、分裂前の点\(D\)における速度がともに\(V\)ですから、
\(L'=Vt+\displaystyle\frac{4}{3}Vt\)
いま、\(Vt=\displaystyle\frac{L}{2}\)なので、
\(L'=\displaystyle\frac{L}{2}+\frac{4}{3}・\frac{L}{2}\)
\(L'=\displaystyle\frac{7}{6}L\)
となります。

問7
分裂して水平投射された方の小物体が水平面に落下した直後の速度の水平成分は\(v_D\)と等しいので、点\(E\)における運動量は、
\(p_E=m・\displaystyle\frac{4}{3}V\)
\(p_E=\displaystyle\frac{4}{3}mv_C\cos\theta\)
です。ここから先は運動量と力積の関係を使っても求まりますし、等加速度の公式を使っても解けます。
両方とも解説しておきます。
(ⅰ)運動量の変化と力積の関係より
\(0-\displaystyle\frac{4}{3}mv_C\cos\theta=F\Delta t\)
\(F\)は動摩擦なので、\(F=-\mu mg\)です。よって、
\(-\displaystyle\frac{4}{3}mv_C\cos\theta=-\mu mg t_S\)
\(t_S=\displaystyle\frac{4v_C\cos\theta}{3\mu g}\)
(ⅱ)等加速度運動の公式より
\(v=v_0+at\)
動摩擦力がかかっている間の加速度は、\(ma=F\)より、\(ma=-\mu mg\)、\(a=-\mu g\)なので、
\(0=\displaystyle\frac{4}{3}v_C\cos\theta-\mu gt_S\)
\(\mu g t_S=\displaystyle\frac{4}{3}v_C\cos\theta\)
\(t_S=\displaystyle\frac{4v_C\cos\theta}{3\mu g}\)
となります。
問8
時刻\(t\)を、\(x\)を用いて表すため、等加速度運動の公式を用います。
\(x=v_0t+\displaystyle\frac{1}{2}at^2\) より
\(a=\mu g\)、\(v_0=\displaystyle\frac{4}{3}v_C\cos\theta\) を代入して、
\(x=\displaystyle\frac{4}{3}v_Ct\cos\theta-\frac{1}{2}\mu g t^2\)
\(\displaystyle\frac{1}{2}\mu gt^2-\frac{4}{3}v_C\cos\theta・t+x=0\)
\(\mu gt^2-\displaystyle\frac{8}{3}v_C\cos\theta・t+2x=0\)
解の公式で解きます。
\(t=\displaystyle\frac{\frac{4}{3}v_C\cos\theta-\sqrt{\frac{16}{9}v_C^2\cos^2\theta-2\mu gx}}{\mu g}\)
プラスマイナスのうち、プラスの方の解は\(a=-\mu g\)で\(x\)に再び戻ったときを示す解なので、不適です。
\(t=\displaystyle\frac{1}{\mu g}\left(\displaystyle\frac{4}{3}v_C\cos\theta-\frac{4}{3}v_C\cos\theta\sqrt{1-\frac{9・2\mu gx}{16v_C^2\cos\theta}}\right)\)
\(t=\displaystyle\frac{4v_C\cos\theta}{3\mu g}\left(1-\sqrt{1-\frac{9\mu gx}{8v_C^2\cos^2\theta}}\right)\)
となり、かなり複雑な解ですが、これが正解のようです。
問9
最終的な力学的エネルギーはゼロですので、点\(A\)における位置エネルギーと、小物体の内部に仕込まれているバネの弾性エネルギーの和を求めればいいことになります。
点\(A\)における位置エネルギー(=点\(C\)における運動エネルギー)を\(E_1\)とすると、
\(E_1=mg(2R+h)=\displaystyle\frac{1}{2}mv_C^2\)
内部に仕込まれているバネの弾性エネルギーを\(E_2\)とすると、衝突前後における力学的エネルギー保存則より、
\(\displaystyle\frac{1}{2}m(v_C\cos\theta)^2+E_2=0+\frac{1}{2}・\frac{3}{4}mv_D^2\)
右辺の第一項は分裂した小物体のうち、\(\displaystyle\frac{1}{4}m\)の分、第二項は\(\displaystyle\frac{3}{4}m\)の分を意味しています。さらに、\(v_D=\displaystyle\frac{4}{3}V=\frac{4}{3}v_C\cos\theta\)を代入して整理すると、
\(\displaystyle\frac{1}{2}m(v_C\cos\theta)^2+E_2=\frac{1}{2}・\frac{3}{4}m・\left(\frac{4}{3}v_C\cos\theta\right)^2\)
\(=\displaystyle\frac{1}{2}・\frac{4}{3}m(v_C\cos\theta)^2\)
\(E_2=\displaystyle\frac{1}{2}・\frac{4}{3}m(v_C\cos\theta)^2-\frac{1}{2}m(v_C\cos\theta)^2\)
\(=\left(\displaystyle\frac{4}{3}-1\right)・\displaystyle\frac{1}{2}m(v_C\cos\theta)^2\)
\(=\displaystyle\frac{1}{3}・\frac{1}{2}mv_C^2\cos^2\theta\)
\(=\displaystyle\frac{1}{3}E_1\cos^2\theta\)
よって、失われた力学的エネルギーの和は
\(E_1+E_2=E_1+\displaystyle\frac{1}{3}E_1\cos^2\theta\)
\(=E_1\left(1+\displaystyle\frac{1}{3}\cos^2\theta\right)\)
\(=mg(2R+h)\left(1+\displaystyle\frac{1}{3}\cos^2\theta\right)\)
となります。
