■解答
問1 \(T_B=\displaystyle\frac{T_0}{2}\) 問2 \(Q_1=-\displaystyle\frac{5}{4}RT_0\) 問3 \(T_C=\displaystyle\frac{\alpha^{1-\gamma^{-1}}}{2}T_0\)
問4 \(z_D=\alpha^{-\gamma^{-1}}L\) 問5 \(Q_2=\displaystyle\frac{5}{4}\alpha^{1-\gamma^{-1}}RT_0\) 問6 \(e=1-\alpha^{\gamma^{-1}-1}\)
問7 \(\alpha_{min}=4\sqrt{2}\) 問8 \(l-x\sin\theta\) 問9 \(\displaystyle\frac{\lambda}{\sin\theta}\)
問10 \(\Delta x_1=\displaystyle\frac{2D}{\sin\theta}\) 問11 \(\Delta x_2=\displaystyle\frac{2\alpha L}{\sin\theta}\) 問12 \(I(x)=E_0^2\left( 1+ \cos\displaystyle\frac{2\pi x \sin\theta}{\lambda} \right)\)
■解説
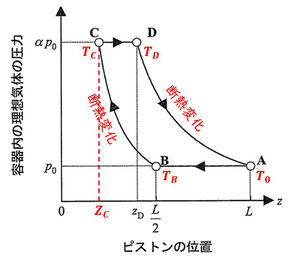
先に条件から分かりそうな情報をいろいろと書き出してしまいましょう。
まず、単原子分子の理想気体を扱っているので
定積モル比熱 \(C_V=\displaystyle\frac{3}{2}R\)
定圧モル比熱 \(C_p=\displaystyle\frac{5}{2}R\)
を用いることができます。
また、図中の状態\(B\)、\(C\)、\(D\)における温度をそれぞれ\(T_B\)、\(T_C\)、\(T_D\)としておき、状態\(C\)におけるピストンの位置を\(Z_C\)としておきます。
ピストンの断面積は\(S\)とします。
問1
状態\(AB\)間で、ボイルシャルル則を適用して
\(\displaystyle\frac{p_0LS}{T_0}=\frac{P_0\frac{L}{2}S}{T_B}\)
\(T_B=\displaystyle\frac{T_0}{2}\)
問2
過程\(A\rightarrow B\)は定圧変化なので、
\(Q=nC_p\Delta T\) より
\(Q=1・\displaystyle\frac{5}{2}R\left(\frac{T_0}{2}-T_0\right)\)
\(Q=-\displaystyle\frac{5}{4}RT_0\) (放熱)
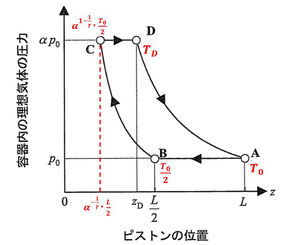
問3
状態\(BC\)間で、ポアソン則を適用して
\(p_0\left(\displaystyle\frac{L}{2}S\right)^{\gamma}=\alpha p_0(Z_CS)^{\gamma}\)
\(\left(\displaystyle\frac{L}{2}\right)^{\gamma}=\alpha Z_C^{\gamma}\)
\(Z_C^{\gamma}=\alpha^{-1}\left(\displaystyle\frac{L}{2}\right)^{\gamma}\)
両辺\(\gamma\)乗根とって(指数を\(\frac{1}{\gamma}\)倍して)
\(Z_C=\alpha^{-\frac{1}{\gamma}}\displaystyle\frac{L}{2}\)
状態\(BC\)間で、ボイルシャルル則を適用して
\(\displaystyle\frac{p_0(\frac{L}{2}S)}{\frac{T_0}{2}}=\frac{\alpha p_0・Z_CS}{T_C}\)
\(\displaystyle\frac{L}{T_0}=\frac{\alpha Z_C}{T_C}\)
\(T_C=\displaystyle\frac{\alpha Z_C}{L}T_0\)
\(T_C=\displaystyle\frac{\alpha}{L}・\alpha^{-\frac{1}{\gamma}}\frac{L}{2}・T_0\)
\(T_C=\alpha^{1-\frac{1}{\gamma}}\displaystyle\frac{T_0}{2}\)
問4
状態\(DA\)間で、ポアソン則を適用して
\(\alpha p_0(Z_DS)^{\gamma}=p_0(LS)^{\gamma}\)
\(\alpha Z_D^{\gamma}=L^{\gamma}\)
\(Z_D^{\gamma}=\alpha^{-1}L^{\gamma}\)
両辺\(\gamma\)乗根とって(指数を\(\frac{1}{\gamma}\)倍して)
\(Z_D=\alpha^{-\frac{1}{\gamma}}L\)
問5
状態\(CD\)間で、ボイルシャルル則を適用して
\(\displaystyle\frac{\alpha p_0・Z_CS}{T_C}=\frac{\alpha p_0・Z_DS}{T_D}\)
\(T_D=\displaystyle\frac{Z_D}{Z_C}T_C\)
\(T_D=\displaystyle\frac{\alpha^{-\frac{1}{\gamma}}L}{\alpha^{-\frac{1}{\gamma}}・\frac{L}{2}}T_C\)
\(T_D=2T_C\)
となります。
つづけて過程\(C\rightarrow D\)では定圧変化なので
\(Q=nC_p\Delta T\) より
\(Q_2=1・\displaystyle\frac{5}{2}R(2T_C-T_C)\)
\(=\displaystyle\frac{5}{2}R・\frac{T_0}{2}\alpha^{1-\frac{1}{\gamma}}\)RT_0\)
\(=\displaystyle\frac{5}{4}\alpha^{1-\frac{1}{\gamma}}RT_0\) (吸熱)
問6
\(A\rightarrow B\rightarrow C\rightarrow D\rightarrow A\)のサイクルにおいて、熱量は、断熱過程\(B\rightarrow C\)、\(D\rightarrow A\)においてはゼロ、\(A\rightarrow B\)において\(Q_1\)(放熱)、\(C\rightarrow D\)において\(Q_2\)(吸熱)であり、気体が外部にした仕事は熱力学第一法則
\(Q=\Delta U +W\) (\(W\)は気体が外部にした仕事) より
\(Q_1+Q_2=0+W\) ――(注)
となるので、
\(e=\displaystyle\frac{W}{Q_2}\)
\(=\displaystyle\frac{Q_1+Q_2}{Q_2}\)
\(=1+\displaystyle\frac{Q_1}{Q_2}\)
\(=1+\displaystyle\frac{-\frac{5}{4}RT_0}{\frac{5}{4}\alpha^{1-\frac{1}{\gamma}}RT_0}\)
\(=1-\displaystyle\frac{1}{\alpha ^{1-\frac{1}{\gamma}}}\)
\(=1-\alpha^{\frac{1}{\gamma}-1}\) (>0)
となります。この値が正であることは、\(\gamma=\frac{5}{3}\)を代入して検算しておくと良いかと思います。熱効率なので負になってはいけません。0~1の範囲でなければその時点でミスです。
(注)
\(Q_1<0\)、\(Q_2>0\)ですが、気体に入る向きを正としているので、単純に加算すればいいことになります。
問7
\(e=1-\alpha ^{\frac{1}{\gamma}-1}≧\displaystyle\frac{1}{2}\)
ここで\(\gamma=\displaystyle\frac{5}{3}\)として
\(1-\alpha ^{\frac{3}{5}-1}≧\displaystyle\frac{1}{2}\)
\(1-\alpha ^{-\frac{2}{5}}≧\displaystyle\frac{1}{2}\)
\(\alpha ^{-\frac{2}{5}}≦\displaystyle\frac{1}{2} (=2^{-1})\)
両辺の指数を(\(-\frac{5}{2}\))倍して
\(\alpha≦2^{\frac{5}{2}}=4\sqrt{2}\)
よって
\(\alpha_{min}=4\sqrt{2}\)
問8
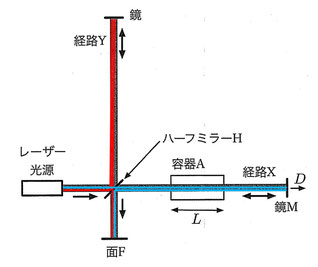
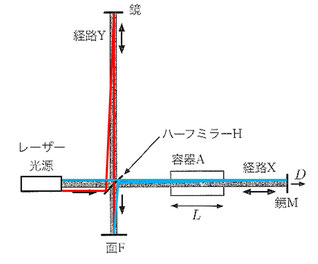
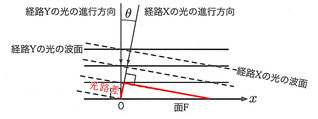
上図のように、ハーフミラーでの反射が90°よりわずかにずれているとき、経路Yの光の進行方向が面に垂直に差し込むのに対して、経路Xの光の進行が若干斜めからの入射となるような条件を作り出すことができます。
経路Xをとおり\(x=0\)に入射する光の光路長は\(l\)であり、経路Xを通り、任意の\(x\)に入射する光は、それよりも\(x\sin\theta\)だけ短くなります。
よって、\(l-x\sin\theta\)
問9
経路Yからきた光の光路長は、全て同じなので、この長さを\(L\)とすると、強め合いの干渉条件は、
\(L-(l-x\sin\theta)=m\lambda\)
\(x=0\)の明線を0次の明線として\(m=0\)とすると、
\(L-l=0\)
となるので、強め合いの干渉条件は
\(x\sin\theta=m\lambda\)
となります。
\(m=0\)のとき、\(x_0\sin\theta=0\)
\(m=1\)のとき、\(x_1\sin\theta=\lambda\)
となるので、
\(\Delta x=x_1-x_0\)
\(=\displaystyle\frac{\lambda}{\sin\theta}\)
問9(別解)
直接求めることもできます。
\(m=0\)のとき
\(L-(l-x_0\sin\theta)=0\)
\(x_0=\displaystyle\frac{l-L}{\sin\theta}\)
\(m=1\)のとき
\(L-(l-x_1\sin\theta)=\lambda\)
\(x_1=\displaystyle\frac{\lambda+l-L}{\sin\theta}=\frac{\lambda}{\sin\theta}+x_0\)
よって
\(\Delta x=x_1-x_0=\displaystyle\frac{\lambda}{\sin\theta}\)
問10
経路Xを通る光の光路長が\(2D\)だけ伸びた、とあるので、
\(l-x\sin\theta \rightarrow l-x\sin\theta+2D\)
と置換すると強め合いの干渉条件は
\(L-(l-x\sin\theta+2D)=m\lambda\)
いま、干渉縞は\(x\)軸に沿って\(\Delta x_1\)だけ動いた、とあるので、
\(m=0\)のとき、\(x=\Delta x_1\)
よって
\(\Delta x_1\sin\theta-2D=0\)
\(\Delta x_1=\displaystyle\frac{2D}{\sin\theta}\)
問11
容器A内の光路長が\((1+\alpha)L\)となるので、往復分も考慮すると、光路長が
\(2[(1+\alpha)L-L]=2(L+\alpha L-L)\)
だけ伸びるので、問10の\(2D\)を\(2\alpha L\)と置換して、同様の手順により
\(\Delta x_2=\displaystyle\frac{2\alpha L}{\sin\theta}\)
問12
経路Yを通る光の電場は
\(E_Y=E_0\sin\omega t\)
\(=E_0\sin 2\pi ft\)
経路Xを通る光の電場は、光路差が\(x\sin\theta\)だけ短いので、
\(t_0=\displaystyle\frac{x\sin\theta}{c}=\frac{x\sin\theta}{f\lambda}\)
だけ早く面Fに到達します。
よって、
\(E_X=E_0\sin\omega(t+t_0)\)
\(=E_0\sin 2\pi f\left(t+\displaystyle\frac{x\sin\theta}{f\lambda}\right)\)
\(=E_0\sin 2\pi \left(ft+\displaystyle\frac{x\sin\theta}{\lambda}\right)\)
ここから
\((E_X+E_Y)^2=E_0^2\left[\sin 2\pi \left(ft+\displaystyle\frac{x\sin \theta}{\lambda}\right)+\sin 2\pi ft\right]^2\)
これに、和→積の公式を適用します
和積の公式は
\(\sin A+\sin B=2\sin \displaystyle\frac{A+B}{2}\cos\frac{A-B}{2}\)
です
\(=E_0^2\left[2\sin 2\pi \displaystyle\frac{(ft+\frac{x\sin\theta}{\lambda})+ft}{2}\cos 2\pi \frac{(ft+\frac{x\sin \theta}{\lambda})-ft}{2}\right]^2\)
\(=4E_0^2\left[\sin \pi \left(2ft+\displaystyle\frac{x\sin\theta}{\lambda}\right)\cos \pi \displaystyle\frac{x\sin \theta}{\lambda}\right]^2\)
\(=4E_0^2\underset{時間平均は\frac{1}{2}}{\underline{\sin^2 2\pi\left(ft+\displaystyle\frac{x\sin\theta}{2\lambda}\right)}}\underset{時間に依存しない}{\underline{\cos^2 \displaystyle\frac{\pi x\sin\theta}{\lambda}}}\)
よって
\(I(t)=4E_0^2・\displaystyle\frac{1}{2}・\cos^2\displaystyle\frac{\pi x \sin\theta}{\lambda}\)
\(I(t)=2E_0^2\cos^2\displaystyle\frac{\pi x\sin\theta}{\lambda}\)