■解答
(あ) \(2dsin\theta\) (い) \(2dsin\theta=k\lambda\) (う) \(cos\theta=ncos\theta'\)
(え) \(\displaystyle\frac{\lambda}{n}\) (お) \(\displaystyle\frac{4\pi d}{\lambda}\sqrt{n^2-cos^2\theta}\) (か) \(2d\sqrt{n^2-cos^2\theta}=k\lambda\)
(き) \(\displaystyle\frac{v_0}{\sqrt{v_0^2-2gs}}\lambda_0\)
問1 \(\displaystyle\frac{2\pi l}{\lambda_0}・\frac{gs}{v_0^2}\)
問2(i) 9回 (ii) \(0.057\)
■解説
(あ) \(2dsin\theta\) 問題ないでしょう。
(い) \(2dsin\theta=k\lambda\) これも問題ないでしょう。
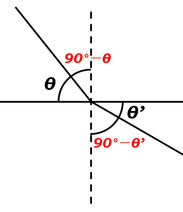
(う) 入射角と屈折角は、面に垂直な線となす角として定義されていますので、注意してください。
スネルの法則(屈折の法則)より、
\(\displaystyle\frac{sin(90°-\theta)}{sin(90°-\theta')}=n\)
\(\displaystyle\frac{cos\theta}{cos\theta'}=n\)
よって
\(cos\theta=ncos\theta'\)
(え) \(\lambda'=\displaystyle\frac{\lambda}{n}\)
見慣れた式ですね。問題ないでしょう。
(お) 経路差は、
\(2ndsin\theta'=2nd\sqrt{1-cos^2\theta')}\)
\(=2nd\sqrt{1-\displaystyle\frac{cos^2\theta}{n^2}}\)
\(=2d\sqrt{n^2-cos^2\theta}\)
であるから、位相差は、
(位相差)\(=\)(経路差)\(×\displaystyle\frac{2\pi}{\lambda}\)
\(=\displaystyle\frac{2\pi}{\lambda}・2d\sqrt{n^2-cos^2\theta}\)
\(=\displaystyle\frac{4\pi d}{\lambda}\sqrt{n^2-cos^2\theta}\)
となります。
経路差から位相差に切り替える最初の1行が重要な関係式で、これまでの京大の入試でも位相差に関わる問題が出てきています。2009年、1989年あたりの波動の問題は参考になるかもしれませんので、どこぞかから入手してきて解いてみることをおススメします。
(私が波動苦手だからなのか、けっこう重たい問題でした…)
(か)
(お)が\(2\pi\)の整数倍のとき、X線が強め合うので、
\(\displaystyle\frac{4\pi d}{\lambda}\sqrt{n^2-cos^2\theta}=2\pi k\)
\(\displaystyle\frac{2d}{\lambda}\sqrt{n^2-cos^2\theta}=k\)
\(2d\sqrt{n^2-cos^2\theta}=k\lambda\)
(き)
質量\(m\)の中性子が\(A\)で散乱(反発)され、辺\(DC\)まで打ちあがるので、位置エネルギーを持つようになる。辺\(AB\)を高さの基準として、力学的エネルギー保存則を立てると、辺\(DC\)での速さを\(v\)として、
\(\displaystyle\frac{1}{2}mv_0^2=\displaystyle\frac{1}{2}mv^2+mgs\)
\(v_0^2=v^2+2gs\)
\(v^2=v_0^2-2gs\)
ド・ブロイ波長の式により
\(\lambda_0\displaystyle\frac{h}{mv_0}\)
\(\lambda'=\displaystyle\frac{h}{mv}\)
であるから、
\(\displaystyle\frac{\lambda'}{\lambda}=\frac{v_0}{v}=\frac{v_0}{\sqrt{v_0^2-2gs}}\)
\(\lambda'=\displaystyle\frac{v_0}{\sqrt{v_0^2-2gs}}\lambda_0\)
問1
経路\(ABCE\)を通る場合と、経路\(ADCE\)を通る場合とでは、\(AD\)間と\(BC\)間での行路差は同じであるから、\(DC\)間と\(AB\)間での行路差を考えるといい。
(位相)\(=\displaystyle\frac{2\pi}{\lambda}×\)(行路長) より
(\(DC\)間の位相)\(=\displaystyle\frac{2\pi}{\lambda'}l\)
(\(AB\)間の位相)\(=\displaystyle\frac{2\pi}{\lambda_0}l\)
よって、両者の位相差を\(\Lambda\)とすると、
\(\Lambda=\displaystyle\frac{2\pi}{\lambda_0}l-\frac{2\pi}{\lambda'}l\)
\(=\displaystyle\frac{2\pi l}{\lambda_0}-\frac{2\pi l\sqrt{v_0^2-2gs}}{v_0\lambda_0}\)
\(=\displaystyle\frac{2\pi l}{\lambda_0}-\frac{2\pi l}{\lambda_0}\sqrt{1-\frac{2gs}{v_0^2}}\)
ここで、\(gs≪v_0^2\)であるから、ルートの部分を近似して、
\(=\displaystyle\frac{2\pi l}{\lambda_0}-\frac{2\pi l}{\lambda_0} \left(1-\frac{gs}{v_0^2} \right)\)
\(=\displaystyle\frac{2\pi l}{\lambda_0}\left[ 1- \left(1-\frac{gs}{v_0^2} \right) \right]\)
\(=\displaystyle\frac{2\pi l}{\lambda_0}・\frac{gs}{v_0^2}\)
問2(i)
問1の結果から、角度\(\alpha\)を\(0→\displaystyle\frac{\pi}{2}\)にする間に、
位相差は\(0→\displaystyle\frac{2\pi lgs}{\lambda_0v_0^2}\)になることが分かった。
\(\Lambda=\displaystyle\frac{2\pi lgs}{\lambda_0v_0^2}\)
に、\(\lambda_0=\displaystyle\frac{h}{mv_0}\)より、\(\displaystyle\frac{1}{v_0^2}=\frac{m^2\lambda_0^2}{h^2}\)を代入すると、
\(\Lambda=\displaystyle\frac{2\pi lgs}{\lambda_0}・\frac{m^2\lambda_0^2}{h^2}\)
さらに、\(\displaystyle\frac{m^2g}{h^2}=6.25×10^13\)、\(ls=10^{-3}\)、\(\lambda_0=1.40×10^{-10}\)を代入すると、
\(\Lambda=2\pi・6.25×10^{13}・10^{-3}・1.40×10^{-10}\)
\(=2\pi×8.75\)
よって、位相差が\(0\)のときも強め合うことを考慮すると、強め合う回数は 9回
問2(ii)
角度\(\alpha\)のとき、位相差は
\(\Lambda=2\pi×8.75×sin\alpha\)
これが、はじめて弱め合うとき、位相差は\(\pi\)であればいいので、
\(2\pi・8.75・sin\alpha=\pi\)
\(17.5sin\alpha=1\)
\(sin\alpha=\displaystyle\frac{1}{17.5}\)
\(=0.05714…\)
\(≒0.057(=5.7×10^{-2})\)
となる。(これは\(\alpha≒3.28°\)に相当する量のようです。)
