■解答
問1 \(x=\displaystyle\frac{mg}{k\cos\theta}\)
問2 \(\sqrt{\displaystyle\frac{kg}{kL\cos\theta+mg}}\)
問3 運動エネルギー \(\displaystyle\frac{mg}{2k}\left( kL\cos\theta+mg \right) \tan^2\theta\) 弾性エネルギー \(\displaystyle\frac{1}{2k}\left( \frac{mg}{\cos\theta}\right)^2\)
問4 \(\displaystyle\frac{1}{2}\left[ \sqrt{ \left( \frac{mg}{kL} \right)+4} -\frac{mg}{kL}\right]<\cos\theta<1\)
問5 \(5.9×10^{-2}kg\)
■解説
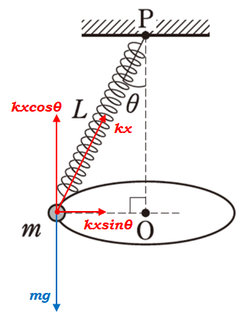
問1
ばねののびを\(x\)とすると、おもりに対する運動方程式の鉛直成分は、鉛直上向きを正として、
\(ma=F\) より
\(0=kx\cos \theta -mg\)
\(kx\cos\theta=mg\)
\(x=\displaystyle\frac{mg}{k\cos\theta}\)
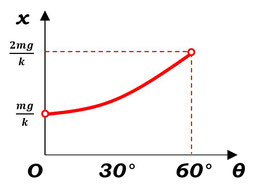
真っ向から増減表を描いて関数の正式な形を導くのは労力がかかりますので、代表的な点を代入してみて、概形を描いていく作戦で勝負しましょう。
\(\theta=0°\) のとき、\(x=\displaystyle\frac{mg}{k}\)
\(\theta=30°\) のとき、\(x=\displaystyle\frac{2mg}{\sqrt{3}k}≒1.15・\frac{mg}{k}\)
\(\theta=60°\) のとき、\(x=\displaystyle\frac{2mg}{k}\)
であることから、グラフの概形は図のようになります。
問2
ばねの長さが\(L+x\)となるので、図から、円運動の半径\(r\)は、
\(r=(L+x)\sin\theta\)
となります。
角速度を\(\omega\)とすると、おもりに対する運動方程式の水平成分は、円の中心に向かう向きを正として、
\(mr\omega^2=F\) より
\(m(L+x)\sin\theta・\omega^2=kx\sin\theta\)
\(m\left(L+\displaystyle\frac{mg}{k\cos\theta}\right)\omega^2 =k・\displaystyle\frac{mg}{k\cos\theta}\)
\(\displaystyle\frac{kL\cos\theta+mg}{k\cos\theta}\omega^2=\frac{g}{\cos\theta}\)
\(\omega^2=\displaystyle\frac{kg}{kL\cos\theta+mg}\)
\(\omega=\sqrt{\displaystyle\frac{kg}{kL\cos\theta+mg}}\)
問3
\(v=r\omega\) より
\(v=(L+x)\sin\theta・\omega\) であるから、
運動エネルギー\(K\)は、
\(K=\displaystyle\frac{1}{2}mv^2\) より
\(K=\displaystyle\frac{1}{2}m\omega^2(L+x)^2\sin^2\theta\)
\(K=\displaystyle\frac{1}{2}m・\frac{kg}{kL\cos\theta+mg}・\left(\displaystyle\frac{kL\cos\theta+mg}{k\cos\theta}\right)^2\sin^2\theta\)
\(K=\displaystyle\frac{1}{2}m・kg・\frac{kL\cos\theta+mg}{k^2}・\tan^2\theta\)
\(K=\displaystyle\frac{mg}{2k}\left(kL\cos\theta+mg\right)\tan^2\theta\)
また、弾性エネルギー\(U\)は、
\(U=\displaystyle\frac{1}{2}kx^2\)
\(U=\displaystyle\frac{1}{2}k\left(\displaystyle\frac{mg}{k\cos\theta}\right)^2\)
\(U=\displaystyle\frac{1}{2k}\left(\displaystyle\frac{mg}{\cos\theta}\right)^2\)
問4
\(K<U\)のとき、問3の結果から、
\(\displaystyle\frac{mg}{2k}(kL\cos\theta+mg)\tan^2\theta<\displaystyle\frac{1}{2k}\left(\displaystyle\frac{mg}{\cos\theta}\right)^2\)
\((kL\cos\theta +mg)\displaystyle\frac{\sin^2\theta}{\cos^2\theta}<\frac{mg}{\cos^2\theta}\)
\((kL\cos\theta+mg)(1-\cos^2\theta)<mg\)
\(\left(\displaystyle\frac{kL}{mg}\cos\theta+1\right)(1-\cos^2\theta)<1\)
\(\displaystyle\frac{kL}{mg}\cos\theta(1-\cos^2\theta)+1-\cos^2\theta<1\)
\(\displaystyle\frac{kL}{mg}\cos\theta(1-\cos^2\theta)-\cos^2\theta<0\)
\(\cos\theta\neq 0\) であるから、両辺から割ると、
\(\displaystyle\frac{kL}{mg}\left(1-\cos^2\theta\right)-\cos\theta<0\)
\(\left(1-\cos^2\theta\right)-\displaystyle\frac{mg}{kL}\cos\theta<0\)
\(\cos^2\theta+\displaystyle\frac{mg}{kL}\cos\theta-1>0\)
ここで
\(\cos^2\theta+\displaystyle\frac{mg}{kL}\cos\theta-1\)\(=0\)
の解は、
\(\cos\theta=\displaystyle\frac{1}{2}\left[-\displaystyle\frac{mg}{kL}+\sqrt{\left( \displaystyle\frac{mg}{kL}\right) +4}\right]\)
であるから、\(0<\cos\theta<1\)において、
\(\displaystyle\frac{1}{2}\left[\sqrt{\left( \displaystyle\frac{mg}{kL}\right) +4}-\frac{mg}{kL}\right]<\cos\theta<1\)
問5
\(k=20N/m\)、\(L=0.10m\)、\(\theta=30°\)、\(g=9.8m/s^2\) のとき、問4の計算過程から、
\(\displaystyle\frac{mg}{2k}(kL\cos\theta+mg)\tan^2\theta=\displaystyle\frac{1}{2k}\left(\displaystyle\frac{mg}{\cos\theta}\right)^2\)
を変形していくと、不等号の部分を等号として同様に式を追っていけばいいことになり、数式部分は同じ形を引っ張ってくることができます。よって、
\(\cos^2\theta+\displaystyle\frac{mg}{kL}\cos\theta-1=0\)
と式変形され、ここに各値を代入していくことにしましょう。すると、
\(\displaystyle\frac{3}{4}+\frac{m×9.8}{20×0.10}×\frac{\sqrt{3}}{2}-1=0\)
両辺\(4\)倍して、
\(3+9.8\sqrt{3}×m-4=0\)
\(9.8\sqrt{3}m=1\)
\(m=\displaystyle\frac{1}{9.8\sqrt{3}}\)
\(=0.05898...\)
\(≒5.9×10^{-2}kg\)
